引言在科技行业中，程序员是一群充满激情和创造力的人。然而，随着时间的推移，当一个程序员超过35岁时，他们可能会面临一些独特的挑战和抉择。这篇博客将讨论超过35岁的程序员应该如何面对职业发展的问题，并提供一些建议和方向。1. 评估技能和经验首先，程序员在职业发展的道路上应该对自己的技能和经验进行评估。超过35岁的程序员通常积累了丰富的经验，这是他们的优势。然而，技术在不断演进，新的编程语言和工具层出不穷。因此，程序员需要时刻保持看书和更新自己的技能。建议：参加培训课程、研讨会和技术会议，以了解最新的技术趋势和发展。投入时间和精力来看书新的编程语言、框架和工具。寻找机会参与开源项目或个人项目，以增加实践经验和展示自己的能力。2. 深化专业领域知识随着经验的积累，超过35岁的程序员可能已经在某个领域有了深入的专业知识。这是一个机会，可以将自己的专业知识进一步加深和扩展。建议：将精力集中在自己感兴趣或擅长的领域，并成为该领域的专家。阅读行业相关的书籍、论文和博客，保持对领域最新发展的了解。参与行业社区，与其他专业人士进行交流和合作。3. 转型到管理或指导角色超过35岁的程序员可以考虑将职业发展的重心转向管理或指导方向。在这个阶段，他们可能已经积累了丰富的实践经验和领导能力，可以成为团队的领导者或技术顾问。建议：探索管理角色的机会，例如项目经理、团队领导或部门负责人。寻找指导他人成长的机会，例如担任导师或教育培训者。建立人际关系网，与其他领导者和专业人士建立联系。4. 创业和独立开发对于有创业精神和独立开发能力的程序员来说，超过35岁也是一个适合追求创业梦想的时机。他们可以利用自己的技术经验和行业洞察，开发自己的产品或服务，并创建自己的公司。建议：评估自己的创业意愿和能力，并制定详细的计划。寻找合作伙伴或团队，共同实现创业目标。探索风险投资和创业支持的机会，以获得资金和资源。5. 协调工作与生活无论是继续在企业工作，转型到管理角色，还是创业，超过35岁的程序员都应该重视协调工作与生活的重要性。过度工作可能会导致疲劳和失去热情，影响职业生涯的长期发展。建议：制定合理的工作时间表，确保有足够的休息和娱乐时间。培养健康的生活作风，包括适当的锻炼和饮食。寻找支持和鼓励的社交圈子，与家人和朋友保持联系。结论超过35岁的程序员在职业发展中可能面临一些独特的挑战，但同时也有许多机会等待着他们。通过评估技能和经验，深化专业领域知识，转型到管理或指导角色，或者追求创业梦想，他们可以找到适合自己的道路。最重要的是，保持看书、协调工作与生活，并享受自己在科技行业中的旅程。希望这篇博客能为超过35岁的程序员提供一些有价值的建议和启发！

统计学，数据挖掘和机器学习中的决策树训练，使用决策树作为预测模型来预测样本的类标。这种决策树也称作分类树或回归树。在这些树的结构里，叶子节点给出类标而内部节点代表某个属性。在决策分析中，一棵决策树可以明确地表达决策的过程。在数据挖掘中，一棵决策树表达的是数据而不是决策。决策树的类型在数据挖掘中，决策树主要有两种类型:    分类树的输出是样本的类标。    回归树的输出是一个实数 (例如房子的价格，病人待在医院的时间等)。术语分类和回归树 (CART) 包含了上述两种决策树, 最先由Breiman 等提出。分类树和回归树有些共同点和不同点—例如处理在何处分裂的问题。有些集成的方法产生多棵树：    装袋算法（Bagging）, 是一个早期的集成方法，用有放回抽样法来训练多棵决策树，最终结果用投票法产生。    随机森林（Random Forest） 使用多棵决策树来改进分类性能。    提升树（Boosting Tree） 可以用来做回归分析和分类决策。    旋转森林（Rotation forest） – 每棵树的训练首先使用主元分析法 (PCA)。还有其他很多决策树算法，常见的有:    ID3算法    C4.5算法    CHi-squared Automatic Interaction Detector (CHAID)， 在生成树的过程中用多层分裂 。    MARS可以更好的处理数值型数据。决策树的优点与其他的数据挖掘算法相比，决策树有许多优点:    易于理解和解释 人们很容易理解决策树的意义。    只需很少的数据准备 其他技术往往需要数据归一化。    即可以处理数值型数据也可以处理类别型 数据。其他技术往往只能处理一种数据类型。例如关联规则只能处理类别型的而神经网络只能处理数值型的数据。    使用白箱 模型. 输出结果容易通过模型的结构来解释。而神经网络是黑箱模型，很难解释输出的结果。    可以通过测试集来验证模型的性能 。可以考虑模型的稳定性。    强健控制. 对噪声处理有好的强健性。    可以很好的处理大规模数据 。缺点    训练一棵最优的决策树是一个完全NP问题。因此, 实际应用时决策树的训练采用启发式搜索算法例如 贪心算法 来达到局部最优。这样的算法没办法得到最优的决策树。    决策树创建的过度复杂会导致无法很好的预测训练集之外的数据。这称作过拟合。 剪枝机制可以避免这种问题。    有些问题决策树没办法很好的解决,例如 异或问题。解决这种问题的时候，决策树会变得过大。 要解决这种问题，只能改变问题的领域或者使用其他更为耗时的学习算法 (例如统计关系学习 或者 归纳逻辑编程).    对那些有类别型属性的数据, 信息增益 会有一定的偏置。参考资料Induction of decisiontrees" Machine Learning An Exploratory Technque for Investigating Large Quantities of Categorical Data  Bias of ImportanceMeasures for Multi-valued Attributes and Solutions  A Survey of Evolutinary Algorithms for Decision-Tree Induction  

随机森林指的是利用多棵树对样本进行训练并预测的一种分类器。该分类器最早由Leo Breiman和Adele Cutler提出，并被注册成了商标。在机器学习中，随机森林是一个包含多个决策树的分类器， 并且其输出的类别是由个别树输出的类别的众数而定。 Leo Breiman和Adele Cutler发展出推论出随机森林的算法。 而 "Random Forests" 是他们的商标。 这个术语是1995年由贝尔实验室的Tin Kam Ho所提出的随机决策森林（random decision forests）而来的。这个方法则是结合 Breimans 的 "Bootstrap aggregating" 想法和 Ho 的"random subspace method"以建造决策树的集合。随机森林的优缺点优点：1.可以用来解决分类和回归问题：随机森林可以同时处理分类和数值特征2.抗过拟合能力：通过平均决策树，降低过拟合的风险性3.只有在半数以上的基分类器出现差错时才会做出错误的预测：随机森林非常稳定，即使数据集中出现了一个新的数据点，整个算法也不会受到过多影响，它只会影响到一颗决策树，很难对所有决策树产生影响缺点：1.据观测，如果一些分类/回归问题的训练数据中存在噪音，随机森林中的数据集会出现过拟合的现象2.比决策树算法更复杂，计算成本更高3.由于其本身的复杂性，它们比其他类似的算法需要更多的时间来训练非常推荐这个学习视频https://education.huaweicloud.com/courses/course-v1:HuaweiX+CBUCNXE086+Self-paced/courseware/45c5a9b65ee348719ddc4f4c3801ad0f/b67e40f52a7447f79364a2de6f2b9398/相关概念1.分裂：在决策树的训练过程中，需要一次次的将训练数据集分裂成两个子数据集，这个过程就叫做分裂。2.特征：在分类问题中，输入到分类器中的数据叫做特征。以上面的股票涨跌预测问题为例，特征就是前一天的交易量和收盘价。3.待选特征：在决策树的构建过程中，需要按照一定的次序从全部的特征中选取特征。待选特征就是在步骤之前还没有被选择的特征的集合。例如，全部的特征是 ABCDE，第一步的时候，待选特征就是ABCDE，第一步选择了C，那么第二步的时候，待选特征就是ABDE。4.分裂特征：接待选特征的定义，每一次选取的特征就是分裂特征，例如，在上面的例子中，第一步的分裂特征就是C。因为选出的这些特征将数据集分成了一个个不相交的部分，所以叫它们分裂特征。

目  录1 AutoML超参优化原理................................................................................................................. 11.1 总体方案.......................................................................................................................................................................................... 11.2 常见的超参数优化方法................................................................................................................................................................ 11.2.1 网格寻优...................................................................................................................................................................................... 11.2.2 随机寻优...................................................................................................................................................................................... 21.2.3 贝叶斯优化.................................................................................................................................................................................. 21.2.3.1 高斯过程（GP）..................................................................................................................................................................... 41.2.3.2 SMAC......................................................................................................................................................................................... 61.2.3.3 TPE.............................................................................................................................................................................................. 61.2.4 BOHB............................................................................................................................................................................................ 72 超参数算法代码实现分析........................................................................................................... 92.1 GPEI................................................................................................................................................................................................ 112.2 SMAC............................................................................................................................................................................................. 132.3 TPE.................................................................................................................................................................................................. 152.4 不同数据规模对算法的影响..................................................................................................................................................... 161 AutoML超参优化原理1.1  总体方案1.2  常见的超参数优化方法1.1 总体方案AutoML基于vega.ml自动化机器学习分析系统，结合自动化工厂，完成大数据各个组件的客户端参数，OS参数，JDK参数的自动调优功能，降低人力消耗，极大的提高参数搜索效率。当前框架中实现的单目标超参数优化算法主要涉及：随机搜索（Random Search）， 贝叶斯优化（Bayesian Optimization, e.g. SMAC, GPEI），TPE（Tree-structured Parzen Estimator）， BOHB（Hyperband with Bayesian Optimization）。1.2 常见的超参数优化方法1.2.1 网格寻优网格化寻优可以说是最基本的超参数优化方法，目的是遍历搜索空间。使用这种技术，我们只需为所有超参数的可能构建独立的模型，评估每个模型的性能，并选择产生最佳结果的模型和超参数。1.2.2 随机寻优随机寻优方法在超参数网格的基础上选择随机的组合来进行模型训练。可以控制组合的数量，基于时间和计算资源的情况，选择合理的计算次数。通常并不是所有的超参数都有同样的重要性，某些超参数可能作用更显著。而随机寻优方法相对于网格化寻优方法能够更准确地确定某些重要的超参数的最佳值。1.2.3 贝叶斯优化贝叶斯优化用于机器学习调参由J. Snoek(2012)提出，主要思想是，给定优化的目标函数(广义的函数，只需指定输入和输出即可，无需知道内部结构以及数学性质)，通过不断地添加样本点来更新目标函数的后验分布(直到后验分布基本贴合于真实分布。简单的说，就是考虑了上一次参数的信息，从而更好的调整当前的参数。他与常规的网格搜索或者随机搜索的区别是：l   贝叶斯调参考虑之前的参数信息，不断地更新先验；网格搜索未考虑之前的参数信息l   贝叶斯调参迭代次数少，速度快；网格搜索速度慢,参数多时易导致维度爆炸l   贝叶斯调参针对非凸问题依然稳健；网格搜索针对非凸问题易得到局部最优表1-1   贝叶斯优化过程中，常见的代理模型（surrogate model）有高斯过程（Gaussian Process），SMAC（基于随机森林），TPE（Parzen Estimator）高斯模型适用于连续型变量的，范围小的参数搜索空间，与此相对的，SMAC是基于随机森林算法的实现，在大范围的搜索空间，离散型变量空间的搜索效率会更好；TPE算法也适用于大范围的搜索空间，离散型变量空间，使用 KDE (核密度估计，带有权重的一维KDEs) 来对密度进行建模。一般形式的Acquisition Funtion是关于x的函数，映射到实数空间R，表示改点的目标函数值能够比当前最优值大多少的概率，目的是权衡当前已有的结果以及探索的可能（balance exploration against exploitation），目前主要有以下几种主流的效用函数（Acquisition function）1.         POI(probability of improvement)2.         Expected Improvement3.         Confidence bound criteria1.2.3.1 高斯过程（GP）介绍贝叶斯优化调参，必须要从两个部分讲起：l   高斯过程，用以拟合优化目标函数l   贝叶斯优化，包括了“开采”和“勘探”，用以花最少的代价找到最优值上图是一张高斯分布拟合函数的示意图，可以看到，它只需要九个点，就可以大致拟合出整个函数形状1.2.3.2 SMAC贝叶斯优化中，除了代理模型(surrogate model)为高斯过程外，另一种用得比较多的代理模型为随机森林SMAC全称Sequential Model-Based Optimization forGeneral Algorithm Configuration，算法在2011被Hutter等人提出。该算法的提出即解决高斯回归过程中参数类型不能为离散的情况。由于随机森林的训练与预测时间复杂度较低，因此在SMAC中可以轻易采样候选点，因此SMAC对真实函数有噪音的情况会更加robust一点；实验表明，当参数空间较复杂且维度较大时，采用SMAC效果会更优一点；随机森林是由很多决策树构成的，不同决策树之间没有关联。当我们进行分类任务时，新的输入样本进入，就让森林中的每一棵决策树分别进行判断和分类，每个决策树会得到一个自己的分类结果，决策树的分类结果中哪一个分类最多，那么随机森林就会把这个结果当做最终的结果。1.2.3.3 TPE贝叶斯优化中，代理模型(surrogate model)还可以是TPE（Tree Parzen Estimator）1.2.4 BOHBBOHB 是由此篇论文提出的一种高效而稳定的调参算法。 BO 是贝叶斯优化（Bayesian Optimization）的缩写，HB 是 Hyperband 算法的缩写。BOHB 依赖 HB（Hyperband）来决定每次跑多少组参数和每组参数分配多少资源（budget），它的改进之处是将 Hyperband 在每个循环开始时随机选择参数的方法替换成了依赖之前的数据建立模型（贝叶斯优化）进行参数选择。 一旦贝叶斯优化生成的参数达到迭代所需的配置数, 就会使用这些配置开始执行标准的连续减半过程（successive halving）。 观察这些参数在不同资源配置（budget）下的表现 g(x, b)，用于在以后的迭代中用作我们贝叶斯优化模型选择参数的基准数据。以上这张图展示了 BOHB 的工作流程。 将每次训练的最大资源配置（max_budget）设为 9，最小资源配置设为（min_budget）1，逐次减半比例（eta）设为 3，其他的超参数为默认值。 那么在这个例子中，s_max 计算的值为 2, 所以会持续地进行 {s=2, s=1, s=0, s=2, s=1, s=0, ...} 的循环。 在“逐次减半”（SuccessiveHalving）算法的每一个阶段，即图中橙色框，都将选取表现最好的前 1/eta 个参数，并在赋予更多计算资源（budget）的情况下运行。不断重复“逐次减半” （SuccessiveHalving）过程，直到这个循环结束。 同时，收集这些试验的超参数组合，使用了计算资源（budget）和其表现（metrics），使用这些数据来建立一个以使用了多少计算资源（budget）为维度的多维核密度估计（KDE）模型。 这个多维的核密度估计（KDE）模型将用于指导下一个循环的参数选择。2 超参数算法代码实现分析当我们对Hive组件的同一个用例（query2）分别用3种不同的算法进行测试后发现结果如下图所示：初步得出的结论是GPEI相对可以比较快速的收敛，SMAC算法的波动比较大，但是最优解相对比较好，TPE的实现偏离预期（Vega的实现有问题，所以后续可以考虑改进）2.1  GPEI2.2  SMAC2.3  TPE2.4  不同数据规模对算法的影响2.1 GPEI高斯过程的质量仅取决于协方差函数。Matern内核的类是RBF的概括。它具有一个附加参数v，用于控制所得函数的平滑度。v越小，近似函数越不平滑。当v趋于无穷，该内核变得等同于RBF内核。如果v=1/2，则Matern内核与绝对指数内核相同。重要的中间值v=1.5是（一次微分函数）和v=2.5（两次微分函数）。针对Hive组件的其中一个用例query，分别采用了v=1.5, v=2.5进行了测试，结果如下图，发现两者差别没有特别大，可能由于参数搜索范围比较大，测试迭代次数不够多，还未达到收敛趋势，后续有待进一步测试。2.2 SMAC针对随机森林算法，我们尝试改变n_estimators和max_depth来改变树的颗树和深度，进而影响模型的训练过程（因为数据量偏少的时候容易造成欠拟合的情形，因此可以减少树的深度和颗树），验证结果如下图所示：在Hive组件，query1这个用例的测试结果上发现，n_estimator=200, max_depth=5的时候效果比较理想，相对收敛会快一点，因此可以改变原先默认的参数设置。2.3 TPE和Vega开发人员初步确认，发现他们的TPE算法开发可能存在漏洞，最后没有达到预期的效果。因此我们考虑变化acquisition function，我们考虑使用POI（Probability of Improvement）替代EI进行测试，测试结果如下图所示，发现使用POI后，算法的效果得到了明显的提升。2.4 不同数据规模对算法的影响我们采用同一个算法模型的相同的参数，对不同数据规模进行了测试，借此来评估数据规模或者集群计算节点数量是否会对算法模型的参数造成影响，以下是对SMAC和GPEI两个算法分别作出的实践。数据量规模：small: 310M    large：3.0G    huge：30.3G    gigantic：303.5G    bigdata: 606.9G double bigdata: 3.0T对SMAC各个数据集规模做了测试，发现在不同数据集规模上用相同的树深和树的数量，最后呈现的趋势是类似的，基本可以说明SMAC算法不会很明显的受到数据规模或者集群计算节点数量的变化。类似的，对GPEI各个数据集规模做了测试，发现在不同数据集规模上用相同的核函数，最后呈现的趋势也是类似的，也基本可以说明GPEI算法不会很明显的受到数据规模或者集群计算节点数量的变化。

　　作为新兴起的、高度灵活的一种机器学习算法，随机森林（Random Forest，简称RF）拥有广泛的应用前景，从市场营销到医疗保健保险，既可以用来做市场营销模拟的建模，统计客户来源，保留和流失，也可用来预测疾病的风险和病患者的易感性。最初，我是在参加校外竞赛时接触到随机森林算法的。最近几年的国内外大赛，包括2013年百度校园电影推荐系统大赛、2014年阿里巴巴天池大数据竞赛以及Kaggle数据科学竞赛，参赛者对随机森林的使用占有相当高的比例。此外，据我的个人了解来看，一大部分成功进入答辩的队伍也都选择了Random Forest 或者 GBDT 算法。　　所以可以看出，Random Forest在准确率方面还是相当有优势的。　　那说了这么多，那随机森林到底是怎样的一种算法呢？　　如果读者接触过决策树（Decision Tree）的话，那么会很容易理解什么是随机森林。随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于机器学习的一大分支——集成学习（Ensemble Learning）方法。随机森林的名称中有两个关键词，一个是“随机”，一个就是“森林”。“森林”我们很好理解，一棵叫做树，那么成百上千棵就可以叫做森林了，这样的比喻还是很贴切的，其实这也是随机森林的主要思想--集成思想的体现。　　其实从直观角度来解释，每棵决策树都是一个分类器（假设现在针对的是分类问题），那么对于一个输入样本，N棵树会有N个分类结果。而随机森林集成了所有的分类投票结果，将投票次数最多的类别指定为最终的输出，这就是一种最简单的 Bagging 思想。

　　随机森林看起来是很好理解，但是要完全搞明白它的工作原理，需要很多机器学习方面相关的基础知识。在本文中，我们简单谈一下，而不逐一进行赘述，如果有同学不太了解相关的知识，可以参阅其他博友的一些相关博文或者文献。1）信息、熵以及信息增益的概念 　　这三个基本概念是决策树的根本，是决策树利用特征来分类时，确定特征选取顺序的依据。理解了它们，决策树你也就了解了大概。　　引用香农的话来说，信息是用来消除随机不确定性的东西。当然这句话虽然经典，但是还是很难去搞明白这种东西到底是个什么样，可能在不同的地方来说，指的东西又不一样。对于机器学习中的决策树而言，如果带分类的事物集合可以划分为多个类别当中，则某个类（xi）的信息可以定义如下:I(x)用来表示随机变量的信息，p(xi)指是当xi发生时的概率。熵是用来度量不确定性的，当熵越大，X=xi的不确定性越大，反之越小。对于机器学习中的分类问题而言，熵越大即这个类别的不确定性更大，反之越小。信息增益在决策树算法中是用来选择特征的指标，信息增益越大，则这个特征的选择性越好。这方面的内容不再细述，感兴趣的同学可以看 《信息&熵&信息增益》 这篇博文。 2）决策树　　决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。常见的决策树算法有C4.5、ID3和CART。3）集成学习　　　集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立地学习和作出预测。这些预测最后结合成单预测，因此优于任何一个单分类的做出预测。　　随机森林是集成学习的一个子类，它依靠于决策树的投票选择来决定最后的分类结果。你可以在这找到用python实现集成学习的文档：Scikit 学习文档。

一、决策树算法简介决策树算法是机器学习的经典算法之一，产生于上世纪六十年代，当下主要分为ID3算法、C4.5算法以及CART算法。ID3算法和C4.5算法核心思想均为通过计算样本信息熵进行分类，两者的区别在于ID3算法基于信息增益作为特征选择的指标，而C4.5则是基于信息增益率作为特征选择的指标，本例中使用ID3算法进行分类。CART算法则是使用基尼指数作为特征选择的指标。二、ID3算法的基本思想ID3算法的核心是统计学中信息熵的概念，通过计算信息熵来判断该数据样本的“纯度”，信息熵越大，数据样本越不“纯”，分类需要的数据量就越大。信息熵的计算公式：info(D)info(D)=-\displaystyle\sum_{i=1}^{k} p_i*\log_2(p_i)i=1∑k​pi​∗log2​(pi​)其中p_ipi​是概率下面介绍一下ID3算法的步骤1.计算类别信息熵将所得到的数据集按照类别逐个计算其信息熵再相加，假设在数据集D中有k个类别，且第i个类别在数据集中所占的概率为p_ipi​，则信息类别熵为：info(D)info(D)=-\displaystyle\sum_{i=1}^{k} p_i*\log_2(p_i)i=1∑k​pi​∗log2​(pi​)2.计算每个特征的信息熵将数据集根据某个特征进行分类后，计算该种特征的条件下各种类别的类别信息熵，也称条件熵。假设将数据集按照特征A进行分类，且A有m个类别，则其计算公式为：info_A(D)infoA​(D)=-\displaystyle\sum_{j=1}^{m} |D_j|/|D|*info(D_j)j=1∑m​∣Dj​∣/∣D∣∗info(Dj​)其中的D_jDj​是指数据集的类别在A特征的各个类别下的样本数量（注意数据集的类别和A特征的类别是不同的概念，比如要在一个数据集中判断一个人在某天心情的好坏，好和坏就是数据集的类别，而一天中有一个特征是天气，天气的类别是晴天、雨天和阴天，我们要算的是心情好和坏分别在晴天，雨天和阴天中的分布的离散情况）其他特征的条件熵也是相同的计算方法3.计算信息增益通过前面两个步骤我们得到了数据集的信息熵和属于各个特征的条件熵，根据第二个步骤我先进行的分类再进行信息熵（或者说条件熵）的计算，分类之后数据的混乱程度肯定降低，也就是说条件熵会小于数据集的信息熵，信息增益则是条件熵和信息熵之间的差值，用来衡量使用该特征分类的效果好坏，假设用特征A进行分类，其信息增益公式为：Gain(A)Gain(A)=info(D)info(D)-info_A(D)infoA​(D)通常我们选择信息增益最大的特征作为分类的节点三、基于ModelArts平台实现ID3算法1.数据集来源数据集选用的是AIGallery的表格类型数据集《硬盘故障预测数据集》网址链接：https://marketplace.huaweicloud.com/markets/aihub/datasets/detail/?content_id=1b5d6ec0-adc0-4fdd-b03f-fecad119eab52.sklearn实现模型部署#导入相关库 import matplotlib.pyplot as plt import pandas as pd import numpy as np from sklearn.model_selection import train_test_split from sklearn import tree from sklearn.metrics import accuracy_score import time #载入数据集 train_test_set = pd.read_csv("dataset_2020.csv",header=0) data = train_test_set.values #分出标签集和特征集 features = data[::,5::2] lables = data[::,4] features = pd.DataFrame(features) lables = pd.DataFrame(lables) lables = lables.astype("float32") #删去整列都是空值的列 features = features.dropna(axis=1,how="all") #将缺失值用中位数填充 features = np.array(features) for i in range(features.shape[1]): temp = np.array(features)[:,i].tolist() median = np.nanmedian(temp) features[np.argwhere(pd.isna(features[:,i].T)),i] = median features = pd.DataFrame(features,dtype="float32") #分出训练集和测试集 train_features,test_features,train_lables,test_lables = train_test_split(features,lables,test_size=0.33,random_state=0) time_1 = time.time() #选用ID3算法 clf = tree.DecisionTreeClassifier(criterion='entropy', random_state=10, splitter='random', ) clf.fit(train_features,train_lables) time_2 = time.time() print('Training cost:{}s'.format(time_2-time_1)) #预测 test_predict = clf.predict(test_features) time_3 = time.time() print("Predicting cost:{}s".format(time_3-time_2)) #得分 score = accuracy_score(test_lables,test_predict) print("score is {}".format(score)) #学习曲线 scores1 = [] for x in range(4,20): clf = tree.DecisionTreeClassifier(criterion='entropy', random_state=10, #使得每一次生成的树都一样 splitter='random',#分类的特征随机,减少过拟合的可能性 max_depth=x #树的最大深度 ) clf.fit(train_features,train_lables) test_predict = clf.predict(test_features) score = accuracy_score(test_lables,test_predict) scores1.append(score) plt.plot(range(4,20),scores1,color='red',label="max_depth") plt.legend() plt.show() scores2 = [] for y in range(2,30): clf = tree.DecisionTreeClassifier(criterion='entropy', random_state=10, splitter='random', max_depth=18, min_samples_split=y #至少有y个样本才会分枝 ) clf.fit(train_features,train_lables) test_predict = clf.predict(test_features) score = accuracy_score(test_lables,test_predict) scores2.append(score) plt.plot(range(2,30),scores2,color='red',label="min_samples_split") plt.legend() plt.show() #手动调参到目前为止效果最好的参数 clf = tree.DecisionTreeClassifier(criterion='entropy', random_state=10, splitter='random', max_depth=18, min_samples_split=16, ) clf.fit(train_features,train_lables) test_predict = clf.predict(test_features) score = accuracy_score(test_lables,test_predict) print(score) #目前最好的预测得分达到0.78153.部分参数解释tree.DecisionTreeClassifier():criterion：决策树衡量划分质量的方法，默认值为‘gini’（基尼指数），默认值下为CART算法，另外一个可选参数为 ‘entropy’(信息增益),选择此参数为ID3算法。random_state：默认值为 ‘None’，可任意设为一个常数，设为常数时可以简单理解为使得每次运行模型都会得到一个相同的树。splitter：节点划分策略，默认值为 ‘best’(最优划分)，模型会在特征的所有划分点中找出最优的划分点；可选参数有 ‘random’(随机局部最优划分)，模型会随机地在部分划分点中找到局部最优的划分点。'best’适合样本量不大的情况下， 'random’适合样本量比较大的时候,是减少过拟合的方法之一。max_depth:树的最大深度，默认值为 ‘None’,指定模型中树的的最大深度。min_samples_split:内部节点能继续划分所包含的最小样本数，是防止过拟合的方法之一。转自，决策树算法实例操演——基于ModelArts平台（小白机器学习初体验）-云社区-华为云 (huaweicloud.com)

决策树算法是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法。分类算法是利用训练样本集获得分类函数即分类模型(分类器)，从而实现将数据集中的样本划分到各个类中。分类模型通过学习训练样本中属性集与类别之间的潜在关系，并以此为依据对新样本属于哪一类进行预测。

简述：决策树(Decision Tree）是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。在机器学习中，决策树是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系，它是一种监督学习。一．决策树模型首先说明下什么是决策树呢？决策树是一个类似流程图的树结构：每个内部节点(分支节点/树枝节点)表示一个特征或属性，每个树叶节点代表一个分类。在决策树的生长过程中主要会存在的问题是：对于选择分支节点的主观性较强。解决办法：利用信息熵或信息增益解决因为人主观判断问题，只需要计算信息熵或信息增益再排序从而正确分类的过程。信息增益的含义 ：划分数据集前后信息发生的变化。熵：物理学中指物体能量的分布均匀情况，信息熵：对信息的不确定性的度量：公式：H(x)=-sum(plog(p))。信息熵越小，不确定性越小，确定性越大，信息的纯度越高。H(D)是数据集D的熵，计算公式：Ck是在数据集D中出现k类的数量，N是样本的数量，类别的总数。H(D|A) 是特征A对与数据集D的条件熵，其意义是：在子集Di中Y的分布。计算方法是：GainA(A的信息增益)=H_All(总体的信息熵)-H(A)(以A节点作为划分节点的信息熵)决策树中分支节点选择：信息增益大的作为分支节点信息增益越大，信息熵越小，信息不确定性越小，确定性越大，纯度越高。综合之后信息增益的公式：特征A对训练集D的信息增益比gR(D,A)定义为HA(D)刻画了特征A对训练集D的分辨能力，信息增益率改进由于信息增益偏向特征取值较多的不足之处，使用信息增益率进一步划分决策树。以上决策算法：ID3算法-信息增益、C4.5算法-信息增益率。决策树剪枝策略： 先剪枝、后剪枝，用于解决过拟合问题。二．ID3和C4.5划分策略ID3和C4.5算法的划分思想：根据信息增益或信息增益率选择构建决策树的分支节点，依次递归建树。决策树构建的基本步骤：(1)如果所有的属性都被用于划分，直接结束；(2)计算所有特征的信息增益或信息增益率，选择信息增益较大的(如a节点)值对应的特征进行分类；(3)如果使用a节点作为划分节点没有划分完成，接下来使用除去a节点之外的其他特征节点中信息增益较大的进一步进行建立决策树。（递归建立决策树）决策树停止停止生长的条件：如果属性都用于划分，直接结束；如果还有没有被划分的节点，使用多数表决；如果所有样本都已经分类，直接结束；定义最大不纯度进行度量；定义叶子节点的数目；定义分支节点包含的样本个数。三．决策树剪枝决策树是充分考虑了所有的数据点而生成的复杂树，有可能出现过拟合的情况，决策树越复杂，过拟合的程度会越高。决策树的构建过程是一个递归的过层，所以必须确定停止条件，否则过程将不会停止，树会不停生长。先剪枝：提前结束决策树的增长。预剪枝降低了过拟合的风险,减少了决策树的训练时间开销和测试时间开销.带来了欠拟合的风险。后剪枝：是指在决策树生长完成之后再进行剪枝的过程。—— 最小错误剪枝技术(MEP)，悲观错误剪枝(MEP)和代价复杂度剪枝(CCP)泛化性能往往优于预剪枝决策树,训练时间开销比未剪枝的决策树和预剪枝的决策树都要大得多。总结：使用决策树进行分类的优点是非常直观，便于理解，并且执行效率高，执行只需要一次构建，可反复使用。但是对小规模数据集才更有效，而且在处理连续变量时效果不好，较难预测连续字段，在类别较多时，错误增加的比较快。参考文献[1] 陈雷.深度学习与MindSpore实践[M].清华大学出版社：2020.[2] 诸葛越，葫芦娃.百面机器学习[M].人民邮电出版社：2020.[3] 阿斯顿.张，李沐.动手学深度学习[M].人民邮电出版社：2020.

摘要随机森林是集成算法最前沿的代表之一。随机森林是Bagging的升级，它和Bagging的主要区别在于引入了随机特征选择。即：在每棵决策树选择分割点时，随机森林会先随机选择一个特征子集，然后在这个子集上进行传统的分割点选择。随机森林随机森林的构造过程：假如有N个样本，则有放回的随机选择N个样本(每次随机选择一个样本，然后返回继续选择)。这选择好了的N个样本用来训练一个决策树，作为决策树根节点处的样本。当每个样本有M个属性时，在决策树的每个节点需要分裂时，随机从这M个属性中选取出m个属性，满足条件m << M。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性。决策树形成过程中每个节点都要按照上面步骤来分裂（很容易理解，如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性，则该节点已经达到了叶子节点，无须继续分裂了）。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。按照上述步骤建立大量的决策树，这样就构成了随机森林了。在建立每一棵决策树的过程中，有两点需要注意采样与完全分裂。首先是两个随机采样的过程，random forest对输入的数据要进行行、列的采样。对于行采样，采用有放回的方式，也就是在采样得到的样本集合中，可能有重复的样本。假设输入样本为N个，那么采样的样本也为N个。这样使得在训练的时候，每一棵树的输入样本都不是全部的样本，使得相对不容易出现over-fitting。然后进行列采样，从M个feature中，选择m个（m << M）。之后就是对采样之后的数据使用完全分裂的方式建立出决策树，这样决策树的某一个叶子节点要么是无法继续分裂的，要么里面的所有样本的都是指向的同一个分类。一般很多的决策树算法都一个重要的步骤——剪枝，但是这里不这样干，由于之前的两个随机采样的过程保证了随机性，所以就算不剪枝，也不会出现over-fitting。输入：数据集D={(x1,y1),(x2,y2),…,(xm,ym)}；特征子集大小K。步骤：Nß给定数据集D构建节点；If所有样本属于一个类别 thenreturn N；Fß可以继续分类的特征集合；If F 为空 thenreturn N；Fiß从F中随机选择K个特征；N.fß特征Fi中具有最好分割点的特征；N.pßf中最好的分割点；DlßD中N.f值小于N.p的样本子集；DrßD中N.f值不小于N.p的样本子集；Nlß以参数(Dl,K)继续调用本程序；Nrß以参数(Dr,K)继续调用本程序；Return N.输出：一棵随机决策树。随机森林和Bagging以上是随机森林中使用的随机决策树算法。参数K用来控制随机性。当K等于所有特征总数时，构建的决策树等价于传统确定性的决策树；当K=1时，会随机选择一个特征；建议K值为特征数的对数。随机树只在特征选择阶段引入随机性，在选择分割点时不会引入。图a：Bagging的10个基学习器；图b：随机森林的10个基学习器；图c：Bagging；图d：随机森林。随机森林和Bagging在40个UCI数据集上预测错误的对比。每个点为一个数据集，点的坐标为两个对比算法的预测误差。对角线标出两个对比算法相同预测误差的位置。比较了随机森林，Bagging和它们基分类器的决策边界。由图可见随机森林和它的基学习器的决策边界比较灵活，因而具有更好的泛化能力。在高斯数据集上，随机森林的测试错误率为7.85%，而Bagging为8.3%。以上图中比较了随机森林和Bagging在40个UCI数据集上的预测错误。很明显，无论使用剪枝还是未剪枝的决策树，随机森林的预测精度都优于Bagging的结果。集成规模在2个UCI数据集上对随机森林和Bagging的影响。随机森林的收敛性和Bagging相似。随机森林的起始点一般较差，特别是当集成规模为1时，随机特征选择会导致决策树性能退化；但是，它通常可以收敛到很低的测试误差。在训练的阶段，随机森林的收敛比Bagging更快速。这是因为，在决策树的构建阶段，Bagging使用的全量的特征进行分割选择，进而生成确定性的决策树，而随机森林仅需要使用随机选择的特征来生成随机决策树。总结：组合分类器比单一分类器的分类效果好，随机森林（random forest）是一种利用多个分类树对数据进行判别与分类的方法，它在对数据进行分类的同时，还可以给出各个变量（基因）的重要性评分，评估各个变量在分类中所起的作用。[1] 陈雷.深度学习与MindSpore实践[M].清华大学出版社：2020.[2] 诸葛越，葫芦娃.百面机器学习[M].人民邮电出版社：2020.[3] 周志华.机器学习[M].清华大学出版社：2016.

> 前文，我们通过小熊派获取了MPU6050数据，并将数据存储于SD卡中。 本次，我们将小熊派绑于大腿上，分别获取人走路、跑步、上楼梯、坐姿的数据。并对数据进行特征向量衍生，将6个数据衍生为38个数据，通过决策树数算进行模型训练，完成姿态估计。 # 一、准备工作 - 安装anaconda环境，并添加jupyter lab，安装第三方库graphviz - 以及可以获取六轴加速度数据，并存储于数据库 # 二、目标 - 对数据进行处理 - 使用决策树算法对行为进行分类 - 达到90%以上的准确率 # 三、数据获取 我们将小熊派设备绑于大腿上，每200ms获取一次数据并存储于SD卡。   分别获取行走、坐姿、跑步、上楼梯的数据各2000组。 # 四、特征向量衍生 因为我们的行为姿态是一个三维的空间，仅仅从六轴数据中难以找出有价值的数据。对每组数据添加标签，其中0-走路，1-坐姿，2-奔跑，3-上楼梯。 通过观察，人在自然行走时每步的时间间隔最长，为0.7~1s，因此我们以1s为周期，即每5组数据为新的一对。 - 平均值 分别对每对三轴加速度、三轴陀螺仪数据做平均值处理，得到6列数据 在对三轴加速度的三个平均值、三轴陀螺仪的三个平均值相加，得2列数据 - 最大值 分别对每对三轴加速度、三轴陀螺仪数据做最大值处理，得到6列数据 - 最小值 分别对每对三轴加速度、三轴陀螺仪数据做最小值处理，得到6列数据 - 峰峰值 分别对每对三轴加速度、三轴陀螺仪数据做峰峰值处理，得到6列数据 - 方差 分别对每对三轴加速度、三轴陀螺仪数据做方差处理，得到6列数据 - 相关系数 分别对三轴加速度的xy、三轴加速度的yz、三轴加速度的xz、三轴陀螺仪的xy、三轴陀螺仪的yz、三轴陀螺仪的xz做相关系数处理，得到6列数据 综上，一共获得新的38列数据  # 五、模型训练 我们使用jupyter lab进行决策树算法演示 ## 1.导入数据集 ```python import pandas as pd import numpy as np dataset = pd.read_excel('D:\MachineLearning\man\mpu.xlsx') dataset col = dataset.columns.values.tolist() #获取列的名称 datas = np.array(dataset[col[2:-1]]) datas label0_data = dataset.loc[dataset['target']==0] #通过loc函数获取导不同标签的数据 label1_data = dataset.loc[dataset['target']==1] label2_data = dataset.loc[dataset['target']==2] label3_data = dataset.loc[dataset['target']==3] # label3_data data_feature = dataset.iloc[:,[0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]] data_feature data_label = dataset.iloc[:,38] ``` 其中，D:\MachineLearning\man\mpu.xlsx为我数据集的路径。data_feature存放特征值，data_feature存放标签值。 我们查看一下特征值:  ## 2.导入sklearn中的tree ```python from sklearn import tree from sklearn.model_selection import train_test_split ``` ## 3.划分训练集、测试集 我们将数据集分为训练集、测试集，比例为7:3 ```python Xtrain,Xtest,Ytrain,Ytest = train_test_split(data_feature,data_label,test_size=0.3) Xtrain ```  ## 4.训练模型 先忽略我的注释代码，score为测试集的准确率 ```python clf = tree.DecisionTreeClassifier(criterion="entropy" ,random_state=5 # ,splitter="random" ,max_depth = 3 ,min_samples_leaf = 5 ,min_samples_split = 5 ) #默认为gin 不纯度指标,random_state随机数种子控制随机性 clf = clf.fit(Xtrain,Ytrain) score = clf.score(Xtest,Ytest) #返回预测的准确度 #score = clf.score(Xtrain,Ytrain) #返回预测的准确度 #score = clf.score(data_feature,data_label) #clf = clf.fit(data_feature,data_label) score ``` 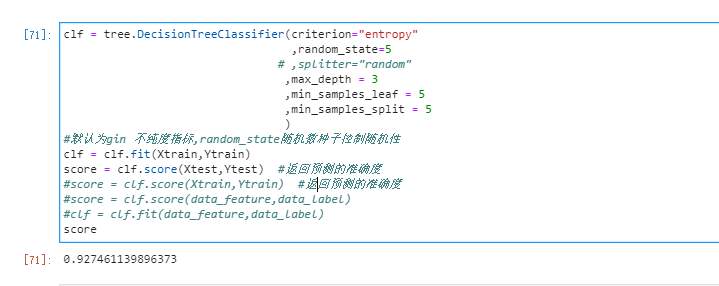 此时，我们看到，测试集的准确率为92% ## 5.画决策树 我们利用graphviz，画出决策树 ```python feature_name = ['a1','a2','a3','a4','a5','a6','a7','a8','a9','a10','a11','a12','a13','a14','a15','a16','a17','a18','a19','a20','a21','a22','a23','a24','25','a26','a27','a28','a29','a30','a31','a32','a33','a34','a35','a36','37','38'] import graphviz dot_data = tree.export_graphviz(clf ,feature_names = feature_name ,class_names = ["走路","坐下","奔跑","上楼梯"] ,filled = True #是否填充颜色，颜色越深，不纯度越低 ,rounded = True #筐的形状 ) graph = graphviz.Source(dot_data) graph ``` 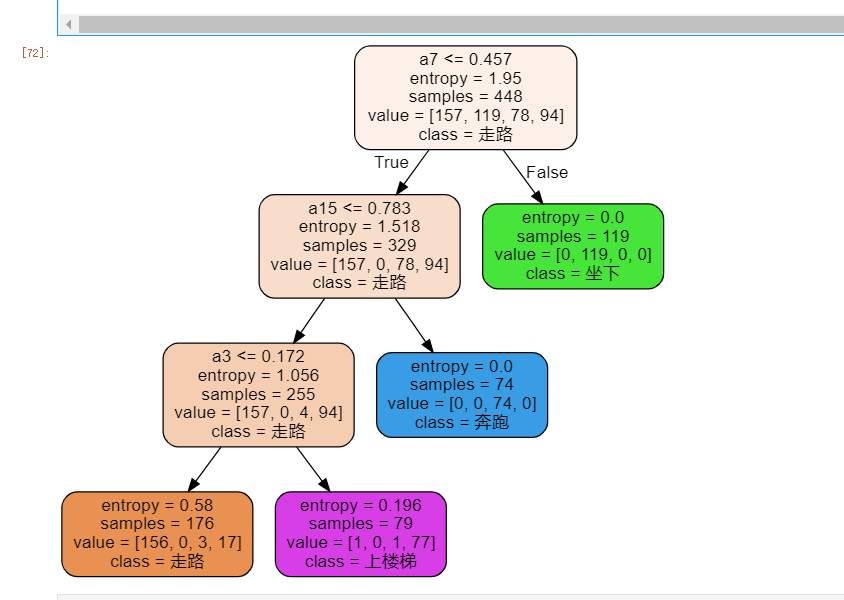 **具体的相关剪枝参数就不再深究，有兴趣的伙伴可以去查找相关资料。** 这是我初步就行剪枝得到的生成树，可以看出此生成树很简单，重要特征值包括三轴加速度的三个平均值之和。下一步，我们将此模型移植到小熊派上，在终端完成行为姿态分类。

决策树的一些优点：易于理解和解释。决策树可以可视化。几乎不需要数据预处理。其他方法经常需要数据标准化，创建虚拟变量和删除缺失值。决策树还不支持缺失值。使用树的花费（例如预测数据）是训练数据点(data points)数量的对数。可以同时处理数值变量和分类变量。其他方法大都适用于分析一种变量的集合。可以处理多值输出变量问题。使用白盒模型。如果一个情况被观察到，使用逻辑判断容易表示这种规则。相反，如果是黑盒模型（例如人工神经网络），结果会非常难解释。即使对真实模型来说，假设无效的情况下，也可以较好的适用。决策树的一些缺点：决策树学习可能创建一个过于复杂的树，并不能很好的预测数据。也就是过拟合。修剪机制（现在不支持），设置一个叶子节点需要的最小样本数量，或者数的最大深度，可以避免过拟合。决策树可能是不稳定的，因为即使非常小的变异，可能会产生一颗完全不同的树。这个问题通过decision trees with an ensemble来缓解。概念难以学习，因为决策树没有很好的解释他们，例如，XOR, parity or multiplexer problems。如果某些分类占优势，决策树将会创建一棵有偏差的树。因此，建议在训练之前，先抽样使样本均衡。

决策树是什么？决策树(decision tree)是一种基本的分类与回归方法。举个通俗易懂的例子，如下图所示的流程图就是一个决策树，长方形代表判断模块(decision block)，椭圆形成代表终止模块(terminating block)，表示已经得出结论，可以终止运行。从判断模块引出的左右箭头称作为分支(branch)，它可以达到另一个判断模块或者终止模块。我们还可以这样理解，分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型：内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性，叶结点表示一个类。蒙圈没？？如下图所示的决策树，长方形和椭圆形都是结点。长方形的结点属于内部结点，椭圆形的结点属于叶结点，从结点引出的左右箭头就是有向边。而最上面的结点就是决策树的根结点(root node)。这样，结点说法就与模块说法对应上了，理解就好。我们回到这个流程图，对，你没看错，这就是一个假想的相亲对象分类系统。它首先检测相亲对方是否有房。如果有房，则对于这个相亲对象可以考虑进一步接触。如果没有房，则观察相亲对象是否有上进心，如果没有，直接Say Goodbye，此时可以说："你人很好，但是我们不合适。"如果有，则可以把这个相亲对象列入候选名单，好听点叫候选名单，有点瑕疵地讲，那就是备胎。不过这只是个简单的相亲对象分类系统，只是做了简单的分类。真实情况可能要复杂得多，考虑因素也可以是五花八门。脾气好吗？会做饭吗？愿意做家务吗？家里几个孩子？父母是干什么的？天啊，我不想再说下去了，想想都可怕。我们可以把决策树看成一个if-then规则的集合，将决策树转换成if-then规则的过程是这样的：由决策树的根结点(root node)到叶结点(leaf node)的每一条路径构建一条规则；路径上内部结点的特征对应着规则的条件，而叶结点的类对应着规则的结论。决策树的路径或其对应的if-then规则集合具有一个重要的性质：互斥并且完备。这就是说，每一个实例都被一条路径或一条规则所覆盖，而且只被一条路径或一条规则所覆盖。这里所覆盖是指实例的特征与路径上的特征一致或实例满足规则的条件。使用决策树做预测需要以下过程：收集数据：可以使用任何方法。比如想构建一个相亲系统，我们可以从媒婆那里，或者通过采访相亲对象获取数据。根据他们考虑的因素和最终的选择结果，就可以得到一些供我们利用的数据了。准备数据：收集完的数据，我们要进行整理，将这些所有收集的信息按照一定规则整理出来，并排版，方便我们进行后续处理。分析数据：可以使用任何方法，决策树构造完成之后，我们可以检查决策树图形是否符合预期。训练算法：这个过程也就是构造决策树，同样也可以说是决策树学习，就是构造一个决策树的数据结构。测试算法：使用经验树计算错误率。当错误率达到了可接收范围，这个决策树就可以投放使用了。使用算法：此步骤可以使用适用于任何监督学习算法，而使用决策树可以更好地理解数据的内在含义。

决策树 (decision tree)，及其变种是一类将输入空间分成不同的区域，每个区域有独立的参数的算法 (Breiman et al., 1984)。如图5.7所示，决策树的每个节点都与输入空间的一个区域相关联，并且内部节点继续将区域分成子节点下的子区域（通常使用坐标轴拆分区域）。空间由此细分成不重叠的区域，叶节点和输入区域之间形成一一对应的关系。每个叶结点将其输入区域的每个点映射到相同的输出。决策树通常有特定的训练算法，超出了本书的范围。如果允许学习任意大小的决策树，那么可以被视作非参数算法。然而实践中通常有大小限制作为正则化项将其转变成有参模型。由于决策树通常使用坐标轴相关的拆分，并且每个子节点关联到常数输出，因此有时解决一些对于逻辑回归很简单的问题很费力。例如，假设有一个二分类问题，当 x2 > x1 时分为正类，则决策树的分界不是坐标轴对齐的。决策树将需要许多节点近似决策边界，坐标轴对齐使其算法步骤将不断来回穿梭于真正的决策函数。

>在物联网边缘技术中，我们希望对收集的数据进行分析。比如我们的智能手环，收集到手腕的三轴加速度、陀螺仪数据，然后我们可以根据训练的模型来判断人的运动状态。本文将讲述如何从零开始实现决策树训练，使用的数据为经典的红酒数据集 # 决策树在sklearn中的实现 **开发环境** - Jupyter lab - Python 3.7.1（你的版本至少要3.4以上 - Scikit-learn 0.20.0 （你的版本至少要0.19 - Graphviz 0.8.4 (没有画不出决策树,安装代码conda install python-graphviz) - Numpy 1.15.3, Pandas 0.23.4, Matplotlib 3.0.1, SciPy 1.1.0 ## SK-leran scikit-learn，又写作sklearn，是一个开源的基于python语言的机器学习工具包。它通过NumPy, SciPy和Matplotlib等python数值计算的库实现高效的算法应用，并且涵盖了几乎所有主流机器学习算法。 官网链接：http://scikit-learn.org/stable/index.html ## 为什么需要SKleran 应用中，用python手写代码来从头实现一个算法的可能性非常低，这样不仅耗时耗力，还不一定能够写出构架清晰，稳定性强的模型。更多情况下，是分析采集到的数据，根据数据特征选择适合的算法，在工具包中调用算法，调整算法的参数，获取需要的信息，从而实现算法效率和效果之间的平衡。而sklearn，正是这样一个可以帮助我们高效实现算法应用的工具包. ## 决策树 决策树（Decision Tree）是一种非参数的有监督学习方法，它能够从一系列有特征和标签的数据中总结出决策规则，并用树状图的结构来呈现这些规则，以解决分类和回归问题。 **决策树算法的核心是要解决两个问题： 1）如何从数据表中找出最佳节点和最佳分枝？ 2）如何让决策树停止生长，防止过拟合？** ### sklearn中的决策树 模块sklearn.tree sklearn中决策树的类都在”tree“这个模块之下。这个模块总共包含五个类： - tree.DecisionTreeClassifier 分类树 - tree.DecisionTreeRegressor 回归树 - tree.export_graphviz 画树 - tree.ExtraTreeClassifier 高随机版本的分类树 - tree.ExtraTreeRegressor 高随机版本的回归树 ### 基本建模流程 - 实例化，建立评估模型对象 - 通过模型接口训练模型 - 提取所需的信息 决策树对应的代码: ```python from sklearn import tree #导入需要的模块 clf = tree.DecisionTreeClassifier() #实例化 clf = clf.fit(X_train,y_train) #用训练集数据训练模型 result = clf.score(X_test,y_test) #导入测试集 ``` ## 重要参数 为了要将表格转化为一棵树，决策树需要找出最佳节点和最佳的分枝方法，对分类树来说，衡量这个“最佳”的指标叫做“不纯度”。通常来说，不纯度越低，决策树对训练集的拟合越好。现在使用的决策树算法在分枝方法上的核心大多是围绕在对某个不纯度相关指标的最优化上。 在同一棵决策树上，叶子节点的不纯度一定是最低的。 Criterion这个参数正是用来决定不纯度的计算方法的。sklearn提供了两种选择： - 输入”entropy“，使用信息熵（Entropy） - 输入”gini“，使用基尼系数（Gini Impurity） 在实际使用中，信息熵和基尼系数的效果基本相同。信息熵的计算比基尼系数缓慢一些，因为基尼系数的计算不涉及对数。另外，因为信息熵对不纯度更加敏感，所以信息熵作为指标时，决策树的生长会更加“精细”，因此对于高维数据或者噪音很多的数据，信息熵很容易过拟合，基尼系数在这种情况下效果往往比较好。当然，这不是绝对的。 ## 实例 —— 建立一棵树 ### 导入所需的模块 ```python from sklearn import tree from sklearn.datasets import load_wine #红酒数据集 from sklearn.model_selection import train_test_split ``` ### 查看数据 ```python wine = load_wine() wine.data.shape wine.target #如果wine是一张表，应该长这样： import pandas as pd pd.concat([pd.DataFrame(wine.data),pd.DataFrame(wine.target)],axis=1) wine.feature_names wine.target_names ```  ### 分测试集和训练集 ``` python Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data,wine.target,test_size=0.3) Xtrain.shape Xtest.shape ``` ### 建立模型 ```python clf = tree.DecisionTreeClassifier(criterion="entropy") clf = clf.fit(Xtrain, Ytrain) score = clf.score(Xtest, Ytest) #返回预测的准确度 score ```  ### 画出生成树 ```python feature_name = ['酒精','苹果酸','灰','灰的碱性','镁','总酚','类黄酮','非黄烷类酚类','花青素','颜 色强度','色调','od280/od315稀释葡萄酒','脯氨酸'] import graphviz dot_data = tree.export_graphviz(clf ,feature_names= feature_name ,class_names=["琴酒","雪莉","贝尔摩德"] ,filled=True ,rounded=True ) graph = graphviz.Source(dot_data) graph ```  ### 探索决策树 ```python #特征重要性 clf.feature_importances_ [*zip(feature_name,clf.feature_importances_)] ``` ### 参数random_state 回到建立模型步骤，score会在某个值附近波动，引起步骤5中画出来的每一棵树都不一样。它为什么会不稳定呢？ 决策树在建树时，是靠优化节点来追求一棵优化的树，但最优的节点能够保证最优的树吗？集成算法被用来解决这个问题：sklearn表示，既然一棵树不能保证最优，那就建更多的不同的树。 即在每次分枝时，不从使用全部特征，而是随机选取一部分特征，从中选取不纯度相关指标最优的作为分枝用的节点 ```python clf = tree.DecisionTreeClassifier(criterion="entropy",random_state=30) clf = clf.fit(Xtrain, Ytrain) score = clf.score(Xtest, Ytest) #返回预测的准确度 score ``` ### random_state & splitter random_state用来设置分枝中的随机模式的参数，默认None;输入任意整数，会一直长出同一棵树，让模型稳定下来。 splitter也是用来控制决策树中的随机选项的，有两种输入值，输入”best"，决策树在分枝时虽然随机，但是还是会优先选择更重要的特征进行分枝（重要性可以通过属性feature_importances_查看），输入“random"，决策树在分枝时会更加随机，树会因为含有更多的不必要信息而更深更大，并因这些不必要信息而降低对训练集的拟合。这也是防止过拟合的一种方式 ```python clf = tree.DecisionTreeClassifier(criterion="entropy" ,random_state=30 ,splitter="random" ) clf = clf.fit(Xtrain, Ytrain) score = clf.score(Xtest, Ytest) score import graphviz dot_data = tree.export_graphviz(clf ,feature_names= feature_name ,class_names=["琴酒","雪莉","贝尔摩德"] ,filled=True ,rounded=True ) graph = graphviz.Source(dot_data) graph ``` ### 剪枝参数 在不加限制的情况下，一棵决策树会生长到衡量不纯度的指标最优，或者没有更多的特征可用为止。这样的决策树往往会过拟合，这就是说，它会在训练集上表现很好，在测试集上却表现糟糕。 ```python #我们的树对训练集的拟合程度如何？ score_train = clf.score(Xtrain, Ytrain) score_train ``` 为了让决策树有更好的泛化性，我们要对决策树进行剪枝。剪枝策略对决策树的影响巨大，正确的剪枝策略是优化决策树算法的核心。 不同的剪枝策略： - max_depth - min_samples_leaf & min_samples_split max_depth 限制树的最大深度，超过设定深度的树枝全部剪掉 min_samples_leaf限定，一个节点在分枝后的每个子节点都必须包含至少min_samples_leaf个训练样本，否则分枝就不会发生，或者，分枝会朝着满足每个子节点都包含min_samples_leaf个样本的方向去发生。 min_samples_split限定，一个节点必须要包含至少min_samples_split个训练样本，这个节点才允许被分枝，否则分枝就不会发生。 ```python clf = tree.DecisionTreeClassifier(criterion="entropy" ,random_state=30 ,splitter="random" ,max_depth=3 ,min_samples_leaf=10 ,min_samples_split=10 ) clf = clf.fit(Xtrain, Ytrain) dot_data = tree.export_graphviz(clf ,feature_names= feature_name ,class_names=["拉菲","嘉露","波尔多"] ,filled=True ,rounded=True ) graph = graphviz.Source(dot_data) graph clf.score(Xtrain,Ytrain) clf.score(Xtest,Ytest) ``` ### 确认最优的剪枝参数 具体怎么来确定每个参数填写什么值呢？这时候，我们就要使用确定超参数的曲线来进行判断了，继续使用我们已经训练好的决策树模型clf。超参数的学习曲线，是一条以超参数的取值为横坐标，模型的度量指标为纵坐标的曲线，它是用来衡量不同超参数取值下模型的表现的线。在我们建好的决策树里，我们的模型度量指标就score。 ```python import matplotlib.pyplot as plt test = [] for i in range(10): clf = tree.DecisionTreeClassifier(max_depth=i+1 ,criterion="entropy" ,random_state=30 ,splitter="random" ) clf = clf.fit(Xtrain, Ytrain) score = clf.score(Xtest, Ytest) test.append(score) plt.plot(range(1,11),test,color="red",label="max_depth") plt.legend() plt.show() ```  ## 分析 每当决策树分枝一次，就有一条线出现。当数据的维度更高的时候，这条决策边界就会由线变成面，甚至变成我们想象不出的多维图形。 当一个模型怎么调整都不行的时候，我们可以选择换其他的模型使用，不要在一棵树上吊死。顺便一说，最擅长月亮型数据的是最近邻算法，RBF支持向量机和高斯过程；最擅长环形数据的是最近邻算法和高斯过程；最擅长对半分的数据的是朴素贝叶斯，神经网络和随机森林。