继续线性回归模型，前面说了如何更新模型参数w，让预测值接近于真实值。现在我们来尝试迭代多次，看看效果。 从w=0开始 ```python #w初始值给0 x,y=0.5,0.8 w=0;lr=0.5 #lr学习率=0.5 pred=x*w loss=((pred-y)**2)/2 grad=(pred-y)*x print('自变量：'+str(x)) print('因变量：'+str(y)) print('初始权重：'+str(w)) print('预测值：'+str(pred)) print('差值：'+str(round(loss,ndigits=3))) print('梯度：'+str(grad)) 自变量：0.5 因变量：0.8 初始权重：0 预测值：0.0 差值：0.32 梯度：-0.4 ``` 然后更新w的值，做第一次迭代： ```python #第一次迭代 w=w-lr*grad pred=x*w loss=((pred-y)**2)/2 grad=(pred-y)*x print('自变量：'+str(x)) print('因变量：'+str(y)) print('权重：'+str(w)) print('预测值：'+str(pred)) print('差值：'+str(round(loss,ndigits=3))) print('梯度：'+str(round(grad,ndigits=3))) 自变量：0.5 因变量：0.8 权重：0.2 预测值：0.1 差值：0.245 梯度：-0.35 ``` 可以看到预测值和真实值的差值在变小（0.32 > 0.245），也就是在向着不断的收敛的方向。

从前面的矩阵乘的代码中可以看出，要写好一个CUDA的代码，需要分配HOST内存（malloc或cudaMallocHost），需要分配DEVICE内存（cudaMalloc），需要将HOST内存数据复制到DEVICE（cudaMemcpy），需要完成GPU核函数的调用，需要把核函数的调用结果在复制回HOST（cudaMemcpy），还需要对前面的各种内存做释放工作（free，cudaFreeHost，cudaFree）。这些工作，虽然是套路，显然还是太繁琐了。于是，聪明的Nvidia在CUDA 6.0以上的版本提出了一个叫做Unified Memory（统一内存）的概念。它把GPU内存、CPU内存在编码层面屏蔽起来：它是可以从系统的任何CPU、GPU访问的单个内存地址空间。它允许应用程序分配可以从CPUs或GPUs上允许的代码读取或者写入数据。具体的方式如下所示：它把原来CPU上的malloc改为cudaMallocManaged，并且分配好的内存地址可以直接被GPU的核函数（图中的 qsort）使用（还记得原来的代码需要先cudaMallocHost/malloc，在cudaMemcpy吗？这里统统不要了。统一内存除了上面使用的 cudaMallocManaged函数来定义变量以外，还可以使用 __managed__ 标识符来表示这是一块统一内存。（这个前面可能还需要再加上 __device__ 标识符供 核函数使用。统一内存使用的时候要借助于 cudaDeviceSynchronize() 来确保CPU和GPU同步。统一内存不显式的区分HOST还是DEVICE的memory，它简化了代码，增强了代码的通用性。统一内存只能在HOST申请。这里面有几个误区需要澄清下：（1）张小白原来以为，只有 Nvidia Jetson Orin那种显存和内存合二为一的设备才有统一内存的概念。但其实并不是——满足 SM架构大于3.0（Kepler架构以上）都可以使用统一内存的方式来编程。逻辑上任何GPU卡或者设备都可以使用统一内存，但是从效果上来看，只有真正的融合为一体的设备（如Jetson AGX Orin），才有最好的统一内存的效果。（2）对于矩阵乘的代码而言，统一内存相当于对Global Memory的一个等效版本，而共享内存则是对SM内部的一种速度优化方式。两者是无关的。也就是说，你在使用统一内存的代码中可以同时使用共享内存。（2）使用了 __managed__ 标识符或 cudaMallocManaged 之后，确实代码中不需要 cudaMalloc,cudaMemcpy这些代码了。但是系统底层其实还会根据情况，决定自己是否需要执行相关的GPU内存分配和 HOST和DEVICE内存的互相拷贝的动作。举个例子，对于张小白的Nvidia Quardo P1000的显卡而言，HOST内存在自己的笔记本内存上（大概有64G），DEVICE内存在GPU显卡（大概有4G）。在这样的环境运行代码，系统仍然会做 申请HOST内存，申请DEVICE内存，HOST内存与DEVICE内存复制等动作。但是对于张小白新购置的了不起的Nvidia AGX Orin而言，HOST内存就是DEVICE内存（大概有32G）。两者不仅仅叫做统一内存，其实还叫做同一内存（张小白自创的）。也就是说，ARM CPU和Nvidia GPU共享一个物理内存。具体的说明可参见：https://zhuanlan.zhihu.com/p/486130961同一内存最大的好处就是：下面典型的三个动作，1、3都可以省略了：所以典型的代码就从左边的模式变成了右边的模式：（1）定义变量：仅需要定义unified memory的变量。节省了空间。（2）HOST->DEVICE：步骤省略（3）执行核函数：跟原来一样（4）DEVICE->HOST：步骤省略（5）显式同步：只是统一内存比原来的方式多一个CPU等待GPU完成的动作。注：上述图片（含代码）来自于上面链接中的文章。那么，统一内存到底是怎么实现的呢？这里借助了下图的做法：CUDA在现有内存池的结构上增加了一个 统一内存系统。开发人员可以直接访问任何内存或者显存资源。当CUDA发现需要访问GPU内存时，如果一开始定义在HOST侧，并且对其进行了初始化，CUDA会自动执行数据拷贝，所以，仍然会受制于PCI-E的带宽和延迟。我们可以看到在这个情况下，代码和运行时变量前后的变迁：好了，概念好像整理得差不多了。下面开始实战：我们把昨天的矩阵乘的代码（包含共享内存优化部分）拿过来，然后看看该怎么优化。原来的代码是这样的：matrix_mul.cuh#pragma once #include <stdio.h> #define CHECK(call) \ do \ { \ const cudaError_t error_code = call; \ if (error_code != cudaSuccess) \ { \ printf("CUDA Error:\n"); \ printf(" File: %s\n", __FILE__); \ printf(" Line: %d\n", __LINE__); \ printf(" Error code: %d\n", error_code); \ printf(" Error text: %s\n", \ cudaGetErrorString(error_code)); \ exit(1); \ } \ } while (0)matrix_mul_old.cu#include <stdio.h> #include <math.h> #include "error.cuh" #include "matrix_mul.cuh" #define BLOCK_SIZE 32 __global__ void gpu_matrix_mult(int *a,int *b, int *c, int m, int n, int k) { int row = blockIdx.y * blockDim.y + threadIdx.y; int col = blockIdx.x * blockDim.x + threadIdx.x; int sum = 0; if( col < k && row < m) { for(int i = 0; i < n; i++) { sum += a[row * n + i] * b[i * k + col]; } c[row * k + col] = sum; } } __global__ void gpu_matrix_mult_shared(int *d_a, int *d_b, int *d_result, int m, int n, int k) { __shared__ int tile_a[BLOCK_SIZE][BLOCK_SIZE]; __shared__ int tile_b[BLOCK_SIZE][BLOCK_SIZE]; int row = blockIdx.y * BLOCK_SIZE + threadIdx.y; int col = blockIdx.x * BLOCK_SIZE + threadIdx.x; int tmp = 0; int idx; for (int sub = 0; sub < gridDim.x; ++sub) { idx = row * n + sub * BLOCK_SIZE + threadIdx.x; tile_a[threadIdx.y][threadIdx.x] = row<n && (sub * BLOCK_SIZE + threadIdx.x)<n? d_a[idx]:0; idx = (sub * BLOCK_SIZE + threadIdx.y) * n + col; tile_b[threadIdx.y][threadIdx.x] = col<n && (sub * BLOCK_SIZE + threadIdx.y)<n? d_b[idx]:0; __syncthreads(); for (int k = 0; k < BLOCK_SIZE; ++k) { tmp += tile_a[threadIdx.y][k] * tile_b[k][threadIdx.x]; } __syncthreads(); } if(row < n && col < n) { d_result[row * n + col] = tmp; } } void cpu_matrix_mult(int *h_a, int *h_b, int *h_result, int m, int n, int k) { for (int i = 0; i < m; ++i) { for (int j = 0; j < k; ++j) { int tmp = 0.0; for (int h = 0; h < n; ++h) { tmp += h_a[i * n + h] * h_b[h * k + j]; } h_result[i * k + j] = tmp; } } } int main(int argc, char const *argv[]) { int m=100; int n=100; int k=100; //声明Event cudaEvent_t start, stop, stop2, stop3 , stop4 ; //创建Event CHECK(cudaEventCreate(&start)); CHECK(cudaEventCreate(&stop)); CHECK(cudaEventCreate(&stop2)); int *h_a, *h_b, *h_c, *h_cc; CHECK(cudaMallocHost((void **) &h_a, sizeof(int)*m*n)); CHECK(cudaMallocHost((void **) &h_b, sizeof(int)*n*k)); CHECK(cudaMallocHost((void **) &h_c, sizeof(int)*m*k)); CHECK(cudaMallocHost((void **) &h_cc, sizeof(int)*m*k)); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { h_a[i * n + j] = rand() % 1024; } } for (int i = 0; i < n; ++i) { for (int j = 0; j < k; ++j) { h_b[i * k + j] = rand() % 1024; } } int *d_a, *d_b, *d_c; CHECK(cudaMalloc((void **) &d_a, sizeof(int)*m*n)); CHECK(cudaMalloc((void **) &d_b, sizeof(int)*n*k)); CHECK(cudaMalloc((void **) &d_c, sizeof(int)*m*k)); // copy matrix A and B from host to device memory CHECK(cudaMemcpy(d_a, h_a, sizeof(int)*m*n, cudaMemcpyHostToDevice)); CHECK(cudaMemcpy(d_b, h_b, sizeof(int)*n*k, cudaMemcpyHostToDevice)); unsigned int grid_rows = (m + BLOCK_SIZE - 1) / BLOCK_SIZE; unsigned int grid_cols = (k + BLOCK_SIZE - 1) / BLOCK_SIZE; dim3 dimGrid(grid_cols, grid_rows); dim3 dimBlock(BLOCK_SIZE, BLOCK_SIZE); //开始start Event cudaEventRecord(start); //非阻塞模式 cudaEventQuery(start); //gpu_matrix_mult<<<dimGrid, dimBlock>>>(d_a, d_b, d_c, m, n, k); gpu_matrix_mult_shared<<<dimGrid, dimBlock>>>(d_a, d_b, d_c, m, n, k); //开始stop Event cudaEventRecord(stop); //由于要等待核函数执行完毕，所以选择阻塞模式 cudaEventSynchronize(stop); //计算时间 stop-start float elapsed_time; CHECK(cudaEventElapsedTime(&elapsed_time, start, stop)); printf("start-》stop：Time = %g ms.\n", elapsed_time); CHECK(cudaMemcpy(h_c, d_c, (sizeof(int)*m*k), cudaMemcpyDeviceToHost)); //cudaThreadSynchronize(); //开始stop2 Event CHECK(cudaEventRecord(stop2)); //非阻塞模式 //CHECK(cudaEventSynchronize(stop2)); cudaEventQuery(stop2); //计算时间 stop-stop2 float elapsed_time2; cudaEventElapsedTime(&elapsed_time2, stop, stop2); printf("stop-》stop2：Time = %g ms.\n", elapsed_time2); //销毁Event CHECK(cudaEventDestroy(start)); CHECK(cudaEventDestroy(stop)); CHECK(cudaEventDestroy(stop2)); //CPU函数计算 cpu_matrix_mult(h_a, h_b, h_cc, m, n, k); int ok = 1; for (int i = 0; i < m; ++i) { for (int j = 0; j < k; ++j) { if(fabs(h_cc[i*k + j] - h_c[i*k + j])>(1.0e-10)) { ok = 0; } } } if(ok) { printf("Pass!!!\n"); } else { printf("Error!!!\n"); } // free memory cudaFree(d_a); cudaFree(d_b); cudaFree(d_c); cudaFreeHost(h_a); cudaFreeHost(h_b); cudaFreeHost(h_c); return 0; }先执行一下：没啥问题。我们来分析一下：上面的代码用到了 h_a, h_b, h_c, h_cc 4个HOST内存，还用到了 d_a, d_b, d_c 三个DEVICE内存。其中，abc是对应的。而cc是放CPU运算结果专用的。其实我们可以把h_cc直接改为malloc的内存就行了。但是为了好看，也可以将这4个HOST内存都改为统一内存。我们将统一内存起名为 u_a, u_b, u_c, u_cc吧！魔改开始：将代码中 h_a->u_a，h_b->u_b，h_c->u_c，h_cc->u_cc，其他变量做相应的适当修改。matrix_mul.cu#include <stdio.h> #include <math.h> #include "error.cuh" #include "matrix_mul.cuh" #define BLOCK_SIZE 32 __managed__ int u_a[100*100]; __managed__ int u_b[100*100]; __managed__ int u_c[100*100]; __managed__ int u_cc[100*100]; __global__ void gpu_matrix_mult(int *a,int *b, int *c, int m, int n, int k) { int row = blockIdx.y * blockDim.y + threadIdx.y; int col = blockIdx.x * blockDim.x + threadIdx.x; int sum = 0; if( col < k && row < m) { for(int i = 0; i < n; i++) { sum += u_a[row * n + i] * u_b[i * k + col]; } u_c[row * k + col] = sum; } } __global__ void gpu_matrix_mult_shared(int *u_a, int *u_b, int *u_result, int m, int n, int k) { __shared__ int tile_a[BLOCK_SIZE][BLOCK_SIZE]; __shared__ int tile_b[BLOCK_SIZE][BLOCK_SIZE]; int row = blockIdx.y * BLOCK_SIZE + threadIdx.y; int col = blockIdx.x * BLOCK_SIZE + threadIdx.x; int tmp = 0; int idx; for (int sub = 0; sub < gridDim.x; ++sub) { idx = row * n + sub * BLOCK_SIZE + threadIdx.x; tile_a[threadIdx.y][threadIdx.x] = row<n && (sub * BLOCK_SIZE + threadIdx.x)<n? u_a[idx]:0; idx = (sub * BLOCK_SIZE + threadIdx.y) * n + col; tile_b[threadIdx.y][threadIdx.x] = col<n && (sub * BLOCK_SIZE + threadIdx.y)<n? u_b[idx]:0; __syncthreads(); for (int k = 0; k < BLOCK_SIZE; ++k) { tmp += tile_a[threadIdx.y][k] * tile_b[k][threadIdx.x]; } __syncthreads(); } if(row < n && col < n) { u_result[row * n + col] = tmp; } } void cpu_matrix_mult(int *u_a, int *u_b, int *u_result, int m, int n, int k) { for (int i = 0; i < m; ++i) { for (int j = 0; j < k; ++j) { int tmp = 0.0; for (int h = 0; h < n; ++h) { tmp += u_a[i * n + h] * u_b[h * k + j]; } u_result[i * k + j] = tmp; } } } int main(int argc, char const *argv[]) { int m=100; int n=100; int k=100; //声明Event cudaEvent_t start, stop, stop2, stop3 , stop4 ; //创建Event CHECK(cudaEventCreate(&start)); CHECK(cudaEventCreate(&stop)); CHECK(cudaEventCreate(&stop2)); //int *h_a, *h_b, *h_c, *h_cc; //CHECK(cudaMallocHost((void **) &h_a, sizeof(int)*m*n)); //CHECK(cudaMallocHost((void **) &h_b, sizeof(int)*n*k)); //CHECK(cudaMallocHost((void **) &h_c, sizeof(int)*m*k)); //CHECK(cudaMallocHost((void **) &h_cc, sizeof(int)*m*k)); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { u_a[i * n + j] = rand() % 1024; } } for (int i = 0; i < n; ++i) { for (int j = 0; j < k; ++j) { u_b[i * k + j] = rand() % 1024; } } //int *d_a, *d_b, *d_c; //CHECK(cudaMalloc((void **) &d_a, sizeof(int)*m*n)); //CHECK(cudaMalloc((void **) &d_b, sizeof(int)*n*k)); //CHECK(cudaMalloc((void **) &d_c, sizeof(int)*m*k)); // copy matrix A and B from host to device memory //CHECK(cudaMemcpy(d_a, h_a, sizeof(int)*m*n, cudaMemcpyHostToDevice)); //CHECK(cudaMemcpy(d_b, h_b, sizeof(int)*n*k, cudaMemcpyHostToDevice)); unsigned int grid_rows = (m + BLOCK_SIZE - 1) / BLOCK_SIZE; unsigned int grid_cols = (k + BLOCK_SIZE - 1) / BLOCK_SIZE; dim3 dimGrid(grid_cols, grid_rows); dim3 dimBlock(BLOCK_SIZE, BLOCK_SIZE); //开始start Event cudaEventRecord(start); //非阻塞模式 cudaEventQuery(start); //gpu_matrix_mult<<<dimGrid, dimBlock>>>(d_a, d_b, d_c, m, n, k); gpu_matrix_mult_shared<<<dimGrid, dimBlock>>>(u_a, u_b, u_c, m, n, k); //开始stop Event cudaEventRecord(stop); //由于要等待核函数执行完毕，所以选择阻塞模式 cudaEventSynchronize(stop); //计算时间 stop-start float elapsed_time; CHECK(cudaEventElapsedTime(&elapsed_time, start, stop)); printf("start-》stop：Time = %g ms.\n", elapsed_time); //CHECK(cudaMemcpy(h_c, d_c, (sizeof(int)*m*k), cudaMemcpyDeviceToHost)); //cudaThreadSynchronize(); //开始stop2 Event CHECK(cudaEventRecord(stop2)); //非阻塞模式 //CHECK(cudaEventSynchronize(stop2)); cudaEventQuery(stop2); //计算时间 stop-stop2 float elapsed_time2; cudaEventElapsedTime(&elapsed_time2, stop, stop2); printf("stop-》stop2：Time = %g ms.\n", elapsed_time2); //销毁Event CHECK(cudaEventDestroy(start)); CHECK(cudaEventDestroy(stop)); CHECK(cudaEventDestroy(stop2)); //CPU函数计算 cpu_matrix_mult(u_a, u_b, u_cc, m, n, k); int ok = 1; for (int i = 0; i < m; ++i) { for (int j = 0; j < k; ++j) { if(fabs(u_cc[i*k + j] - u_c[i*k + j])>(1.0e-10)) { ok = 0; } } } if(ok) { printf("Pass!!!\n"); } else { printf("Error!!!\n"); } // free memory //cudaFree(d_a); //cudaFree(d_b); //cudaFree(d_c); //cudaFreeHost(h_a); //cudaFreeHost(h_b); //cudaFreeHost(h_c); return 0; }执行一下：额，好像速度没啥变化。查看下性能：

一种基于深度学习的物联网信道状态信息获取算法廖勇, 姚海梅, 花远肖重庆大学通信与测控中心，重庆 400044摘要针对基于大规模多输入多输出（MIMO）的物联网系统中用户侧将信道状态信息（CSI）发送到基站时反馈开销大的问题，提出一种基于深度学习的CSI反馈网络用来反馈CSI。该网络首先使用卷积神经网络（CNN）提取信道特征矢量和最大池化层通过降维来达到压缩CSI的目的，然后使用全连接和CNN将压缩的CSI解压，恢复原始信道。仿真结果表明，与现有的CSI反馈方法相比，所提出的CSI反馈网络恢复的CSI更接近原始信道，重构质量明显提高。关键词： 大规模MIMO ; 物联网 ; CSI反馈 ; 深度学习1 引言物联网（IoT，Internet of things）是新一代信息技术的重要组成部分，也是“信息化”时代的重要发展阶段。传统移动通信网络主要解决人与人的互联，而物联网解决的是万物互联[1]。IoT 技术将扮演至关重要的角色，因为IoT技术能够做到机器与机器（M2M，machine to machine）[2]和机器与人的连接，可以极大地促进人类社会发展。目前，有很多技术可以用于IoT信息的传输，如蓝牙、无线局域网和红外线等常见的信息传输方式，IoT 由于其极大的可扩展性和实用性正受到人们越来越多的关注。作为 5G 的关键技术之一，大规模多输入多输出（MIMO，multiple input multiple output）技术正在逐渐变得成熟。该技术与传统MIMO技术相比，在物理特性和性能上存在显著优势，具有高频谱效率和高能量效率等优点。目前，欧洲多国和中国等都在大力发展基于LTE的IoT，随着5G的高速推进，大规模MIMO系统也应用于IoT的典型应用场景中，该系统利用基站（BS，base station）大量发射天线来有效支持多个IoT设备的传输，能够很好地提高系统的频谱效率和能量效率[3,4]。基于大规模MIMO的IoT具有很多优势，但也存在一些技术上的挑战。在基于大规模 MIMO 的IoT系统中，为了保证传输过程的服务质量（QoS， quality of service），发送端通常需要进行预编码、自适应编码等操作。然而，这些操作都需要发送端获得下行信道状态信息（CSI，channel state information），如果没有获得准确的下行CIS，IoT系统将不能对连接的IoT设备提供高QoS的通信服务。因此，发送端获得准确的下行CSI对整个系统的通信性能具有显著影响。目前，国内外学者对发送端获取CSI的方法进行了大量研究，并提出了许多获取CSI的方法。文献[5]使用离散余弦变换（DCT，discrete cosine transform）矩阵作为稀疏矩阵，该方案从减少噪声的角度出发，针对性地研究了基于压缩感知（CS， compressed sensing）的CSI有限反馈方法。文献[6]和文献[7]提出适用于单天线、多用户场景的基于主成分分析（PCA，principal component analysis）降维的压缩反馈方法。文献[8]在 PCA 的基础上，通过自回归预测补偿反馈使 BS 获得 CSI。虽然学者已提出很多CSI反馈方法，但这些方法的反馈精度不高，误差较大。近年来深度学习发展迅速，在处理大数据方面表现出强大的能力，已有研究人员采用深度学习方法来实现CSI反馈。文献[9]提出基于深度学习的大规模MIMO的CSI反馈，利用全连接网络和残差网络（整个网络被命名为CsiNet）来实现CSI压缩和解压。文献[10]在文献[9]中CsiNet的基础上，增加了长短期记忆（LSTM，long short-term memory）网络（整个网络被命名为 CsiNet-LSTM），对时变大规模MIMO信道进行CSI反馈。但是，目前尚没有研究人员将深度学习用于IoT信道场景的CSI反馈。为此，本文针对频分双工（FDD，frequency division duplex）模式下基于大规模 MIMO 的 IoT系统的CSI获取问题展开研究，考虑传统CSI反馈方法的反馈精度不高以及进一步研究深度学习在基于大规模MIMO的IoT系统中CSI获取的适用性，提出一种基于深度学习的CSI反馈算法，主要贡献如下。本文提出一种创新的应用于大规模 MIMO 的IoT系统的基于深度学习的CSI反馈算法，该算法主要利用卷积神经网络（CNN，convolutional neural network）提取信道特征矢量，不同于文献[9]和文献[10]，该算法不是采用全连接网络降维，而是采用最大池化层（maxpooling）降维来压缩数据，通过池化可去掉一些无关紧要的数据，保留最重要的特征，留下最能表达数据特征的信息。与全连接层相比，池化网络不仅可以压缩数据，还可以减少待估计参数的数量。然后使用全连接网络和 CNN 将压缩的CSI解压，从而恢复原始信道。最后，对大规模MIMO的IoT系统中基于深度学习的CSI反馈方法和常用的CSI反馈方法的性能效果进行仿真比较。2 结束语本文提出了一种基于深度学习的网络用于大规模MIMO的IoT系统中的CSI反馈，该网络通过离线训练和深度学习的非线性映射特性能够更好地学习信道结构特点。通过仿真，分析了所提算法在大规模MIMO的IoT系统中CSI反馈的性能表现。从仿真结果可以看出，本文所提出的方法不仅比传统的 CSI 反馈方法运行时间更少，而且具有更高的反馈精度，恢复的 CSI 质量明显提高。下一步将研究 IoT 通信场景中基于深度学习的信道估计的应用。The authors have declared that no competing interests exist.作者已声明无竞争性利益关系。3 原文链接http://www.infocomm-journal.com/wlw/article/2019/2096-3750/2096-3750-3-1-00008.shtml

❤ AI系列往期直播回顾：【GDE直播公开课·第七期】低门槛AI开发模式：ModelFoundry❤ 直播视频回顾videovideovideovideovideovideovideovideovideo❤ 精选问答序号问题回复1AI建模后训练需要多久才能提高准确率？训练时间与所用模型、数据等紧密相关，一般视情况而定。2AI、机器学习、深度学习的关系？这三者是一种包含关系。人工智能是其中最广阔的概念，包含了多种研究学派和研究方向。机器学习是人工智能的子集，笼统来说机器学习主要研究从数据中学习的相关方法。而深度学习又是机器学习的子集，主要指使用了深度神经网络的机器学习方法。3同构和异构怎么定义？异构迁移也是映射到同一特征空间吗？同构和异构的主要区别是，源域和目标域的特征空间是否有交叉重合。目前异构迁移学习大部分是在不同的特征空间之间迁移知识。同时，异构迁移中也往往是进行特征对齐，将源域和目标域映射到同一特征空间上。4既然有了源域数据，如何决定是用迁移学习还是直接用源域数据训练？迁移学习主要目的是解决目标域问题，而源域与目标域是有差别的，直接用源域在目标域效果不太好。5想尝试迁移学习的话，有没有什么好上手的例子？一方面，可以参考相关文献中的MNIST、USPS手写识别数据集，ImageNet、COCO图像类数据集等多种公开数据集；另一方面可以参考阿里和百度的开源工具EasyTransfer和AutoDL-Transfer等。6请问预训练模型加入Adapter层时，down-project和up-project的作用是什么？主要目的是降低Adapter模块的参数数量。7基于特征的迁移学习方法为什么有些也使用了冻结-微调，是不是与基于模型的方法类似？神经网络确实有一定二义性，网络是一个模型，同时又是用来提取特征的。8迁移学习对机子的性能要求高吗？普通电脑能进行训练吗？要看什么场景，如果是传统机器学习，样本量不大是可以的；另外像图像分类、文本分类这些简单的也可以用cpu跑。9通过对直播中迁移学习的介绍，我看见利用到了数据和模型，而且迁移学习在自然语言处理方面有应用场景，那么我想请问老师，在利用数据的方面是否需要像建模比赛那样对数据进行处理（比如：缺失值的填充等），在利用模型方面是否需要像建模比赛一样不断的对模型进行优化以取得最理想的一个结果是的，迁移学习仍然需要对于数据进行必要的数据处理（特征工程）等工作，以提升源域到目标域迁移的性能；同时，模型训练时的一些超参也需要合理的调整，以取得更好的结果。10迁移学习与机器学习关系是什么？与迁移学习在一个层面的其他学习技术有哪些？机器学习包含的范围更广，而迁移学习是众多机器学习方法中的一种。但迁移学习与机器学习中传统的有监督、无监督学习、强化学习等都有所不同，它更强调将源域的模型和知识迁移到目标域中。与迁移学习类似或者相关的机器学习技术还有元学习、多任务学习、增量学习和小样本学习等。分享背景：迁移学习旨在利用数据、任务和模型之间的相似性，将已学习到的模型、知识等应用于新的领域，达到事半功倍的效果。在计算机视觉、自然语言处理、语音识别等方面上迁移学习都具有广泛应用。活动说明：1.有效盖楼：留言“报名”或参与提问/建议或回复暗号的，均可参与盖楼。报名和提问可在同一楼层，也可在不同楼层。盖楼截止时间：8月11日 24:00；2.无效盖楼：复制别人的提问、建议等，以及其他不符合要求的灌水信息皆为无效盖楼。注意：同一用户盖楼不能连续超过3楼，总楼层数不能超过10楼。超过盖楼数将视为无效盖楼；3.无效盖楼且踩中获奖楼层，也将视为无效，奖品不予发放，该楼层奖项轮空；4.楼层总数取值仅限活动期间内，即2022年8月1日至8月11日所盖楼层，其余时间楼层无效；5.鼓励自主撰写建议，复制、改写他人内容将不纳入评选，同样的内容以首发为准；6.为保证活动有序进行，一经发现有作弊行为，将取消奖励资格；7.请务必使用个人账号参与活动；8.所有获奖用户，请于获奖后3日内完成实名认证，否则视为放弃奖励；9.本次活动如一个实名认证对应多个账号，只有一个账号可领取奖励；一个实名认证账号只能对应一个收件人，如同一账号填写多个不同收件人或不同账号填写同一收件人，均不予发放奖励；（举例说明：具备同一证件号（比如身份证号/护照ID/海外驾照ID/企业唯一识别号等）、同一手机号、同一设备、同一IP地址等，均视为同一实名用户）10.所有参加本活动的用户，均视为认可并同意遵守华为云社区的用户协议及隐私政策；11.GDE数智平台可能需要根据活动的实际举办情况对活动规则进行变更；若有变更，将以活动页面告知等方式及时通知；12.活动结束后将在活动帖和【GDE直播交流群】微信群中公布获奖名单，奖品配送范围为中国大陆地区，部分地区或因疫情原因延迟配送；13.GDE数智平台拥有活动解释权。中奖公示（已提供地址的中奖人员，奖品将陆续发出；未提供地址的，请留意私信，工作人员将联系获取地址，请在2022年8月31日前提供地址，过时视为自动放弃礼品）请各位中奖者微信添加：华为GDE官方小助手（gdezhushou），回复：GDE直播公开课提供邮寄地址，不添加不能获奖哦~小助手微信二维码报名有奖楼层昵称奖品16yd_231481371GDE定制鼠标垫38yd_234511385GDE定制鼠标垫59DragonCurryGDE定制鼠标垫81madqfrogGDE定制鼠标垫103相信光的奥特王小懒GDE定制鼠标垫探讨有奖昵称优秀提问奖品相信光的奥特王小懒通过对直播中迁移学习的介绍，我看见利用到了数据和模型，而且迁移学习在自然语言处理方面有应用场景，那么我想请问老师，在利用数据的方面是否需要像建模比赛那样对数据进行处理（比如：缺失值的填充等），在利用模型方面是否需要像建模比赛一样不断的对模型进行优化以取得最理想的一个结果？帆布袋HB1688迁移学习与机器学习关系是什么？与迁移学习在一个层面的其他学习技术有哪些？帆布袋组队有奖小组暗号发送人数组长奖品AI学习12suifeng1324GDE定制大礼包举一反三5cauxiaoweiGDE定制大礼包暗号4OpenRunGDE定制大礼包*获奖小组由组长领取礼包自行分发，小组名单以回帖的为准直播口令奖排名昵称奖品1user_beifengGDE定制玩偶2匿名用户GDE定制玩偶3madqfrogGDE定制玩偶暖场互动奖互动昵称奖品第一轮聚***酯GDE定制冰箱贴第二轮赤*GDE定制防晒伞第三轮Y***LGDE定制玩偶

继续线性回归模型，这里先说`随机梯度下降法`。 先考虑一个简单的模型，没有截距，只有一个自变量： y=xw 当观测点为(x=0.5,y=0.8),w=3时，残差平方和是 ```python x,y=0.5,0.8 w=3 rss=(y-x*w)**2/2 print(rss) #0.24499999999999997 ``` `梯度`（gradient）记作$\nabla$，函数RSS(w)关于参数w的梯度，记作$\nabla_wRSS(w)$，简洁的记作$\nabla_w$ 。它是RSS(w)关于w的偏导数，即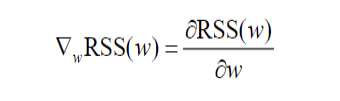：  对于这里的简单模型，就有：  所以w=3时，$\nabla_w$=(0.5x3-0.8)x0.5=0.35 梯度就是w=3处的切线的斜率，这里梯度是正。如下图 ```python pred=x*w grad=(pred-y)*x print('w=3时，预测值：'+str(pred)) print('w=3时，残差平方和：'+str(round(rss,ndigits=3))) print('w=3时，RSS(w)的梯度：'+str(grad)) #w=3时，预测值：1.5 #w=3时，残差平方和：0.245 #w=3时，RSS(w)的梯度：0.35 w_vec=np.linspace(-1,4,100) rss_vec=[] for w_tmp in w_vec: rss_tmp=(y-x*w_tmp)**2/2 rss_vec.append(rss_tmp) plt.plot(w_vec,rss_vec) plt.scatter(w,rss,s=100,c='y',marker='o') plt.plot(np.linspace(2.5,3.5,50),\ np.linspace(2.5,3.5,50)*0.35-0.805,\ '--',linewidth=2.0) plt.xlabel('w',fontsize=16) plt.ylabel('RSS',fontsize=16) #ax=plt.gca() #ax.set_aspect(1) plt.show() ```  这个切线的斜率看上去不是0.35的样子啊，明显要更陡一下。这是因为x轴和y轴的比例不一致而导致的视觉效果，如果轴的比例之后显示是这样的，这样看上去就对了  这里预测值大于实际值，差值是0.7，很自然的，要让预测值更接近实际值的话，需要让预测值变小。想让预测值变小，很简单的就让w变小，变小多少呢？这里的梯度是一个正值，那就先变小一个梯度呗。也就是w-grad。 来看一下梯度为负的情况。当w=0时， ```python x,y=0.5,0.8 w=0 ​ pred=x*w rss=(pred-y)**2/2 grad=(pred-y)*x print('w=0时，预测值：'+str(pred)) print('w=0时，残差平方和：'+str(round(rss,ndigits=3))) print('w=0时，RSS(w)的梯度：'+str(grad)) #w=0时，预测值：0.0 #w=0时，残差平方和：0.32 #w=0时，RSS(w)的梯度：-0.4 ``` ```python plt.plot(w_vec,rss_vec) plt.scatter(w,rss,s=100,c='y',marker='o') plt.plot(np.linspace(-0.5,0.5,50),\ np.linspace(-0.5,0.5,50)*(-0.4)+0.32,\ '--',linewidth=2.0) plt.xlabel('w',fontsize=16) plt.ylabel('RSS',fontsize=16) #ax=plt.gca() #ax.set_aspect(1) plt.show() ```  当w=0时，预测值小于真实值0.8。很自然的，要让预测值更接近实际值的话，需要让预测值变大。想让预测值变大，很简单的就让w变大，变大多少呢？这里的梯度是一个负值，那就先变大一个负的梯度呗。就是w+(-grad)，巧了，也是w-grad。 所以无论w的初始值是在哪边，$w=w-\nabla_wRSS(w)$ 都可以让w朝着RSS变小的方向移动。RSS最小的地方，就是我们寻找的地方，因为在这个地方预测值和真实值的差异最小，也就是说预测值最接近真实值。  这个算法就是梯度下降法，在更新w的过程中，加入了一个系数$\alpha$，他是一个比较小的正数，叫做`学习步长`，这样可以让w更新的速度变慢一些，使得w更容易收敛。

继续线性模型， 有了预测值，和真实值比较一下，就知道预测结果准确不准确？用预测值减去真实值 $\hat{y}-y$ ，如果是正数，说明预测值偏高，如果是负数说明偏低。通常使用差的平方来衡量预测误差。 ```python target=ad.values[0][3] loss=(pred-target)**2 print(loss) #466.9921 ``` 而用残差平方之和，可以用来衡量模型总的预测误差。 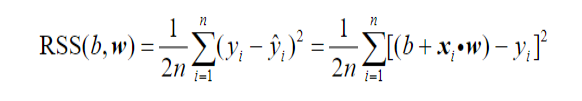 ```python rss=0 for i in range(len(ad)): input=ad.values[i][0:3] pred=linear_mode(input,w,b) target=ad.values[i][3] rss+=(pred-target)**2/2/len(ad) print(rss) #143.69051025000013 ``` 这里乘以常数1/2，说是为了稍后估计b和w方便一些。 很自然的，我们要最小化 $RSS(b,w)$，得到这种情况下b和w的估计值。  $RSS(b,w)$ 也叫做目标函数或者损失函数，它值叫做预测误差或者模型误差。求它的最小值的方法有很多，最常见的方法是`求偏导数`，然后令这些偏导数等于零，解方程得到b和w的估计值。但是这个方法只适合少数结构比较简单的模型（比如线性回归模型），不能求解深度学习这类复杂模型的参数。 所以下面介绍的是深度学习中常用的优化算法：`梯度下降法`。其中有三个不同的变体：随机梯度下降法、全数据梯度下降法、和批量随机梯度下降法。

下面是一个简单的例子来介绍线性回归模型。 数据是在多个市场的3个不同渠道的广告投入以及商品销量。 这个模型的意义也就很明白了，那就是找出在这3个不同渠道广告投入与最终的商品销量之间的关系。 先把数据可视化： ```python %config InlineBackend.figure_format='retina' import pandas as pd import matplotlib.pyplot as plt import numpy as np ad = pd.read_csv('./Ad.csv') ad.head() ```  ```python plt.scatter('TV','sales',data=ad,label='TV',marker='D') plt.scatter('radio','sales',data=ad,marker='o',label='radio') plt.scatter('newspaper','sales',data=ad,marker='s',label='newspaper') plt.legend(loc='lower right') plt.xlabel('Advertising Budgets',fontsize=16) plt.ylabel('Sales',fontsize=16) plt.show ```  再来看一下数学上对这些数据的表达， 第1个观测点的输入向量 x1=(x11,x12,x13)， 第2个观测点的输入向量 x2=(x21,x22,x23) 那么因变量矩阵X表示为：  因变量向量y表示为：  前一节已经讲过线性回归模型的数学公式的表达，这里我们先假设给定截距项b和自变量权重w，至于误差这里不管，那么我们就可以写出预测函数了。 ```python def linear_mode(input,weight,b): prediction=np.sum(input*weight)+b return prediction b=10 w=np.array([0.1,0.1,0.1]) input_0=ad.values[0][0:3] print('第一个观测点的自变量向量：'+str(input_0)) pred=linear_mode(input_0,w,b) print('第一个观测点的预测值：'+str(pred)) ``` ```html 第一个观测点的自变量向量：[230.1 37.8 69.2] 第一个观测点的预测值：43.71 ```

每天学习一点点几何深度学习，是从对称性和不变性的角度对广义机器学习问题进行几何统一的尝试，其原理不仅是卷积神经网络的突破性性能和图神经网络近期成功的基础，也为构建新型的、面向特定问题的归纳偏置提供了一种有原则的方法。2022 年的 GDL100 共包含 12 节常规课程、3 节辅导课程和 5 次专题研讨。12 节常规课程主要介绍了几何深度学习的基本概念知识，包括高维学习、几何先验知识、图与集合、网格（grid）、群、测地线（geodesic）、流形（manifold）、规范（gauge）等。3 节辅导课主要面向表达型图神经网络、群等变神经网络和几何图神经网络。Michael Bronstein 是几何深度学习的先驱，他与 Joan Bruna、Taco Cohen、Petar Veličković共同撰写的《几何深度学习》是领域内的经典必读书目。除了出书，这几位作者还联合在非洲数学科学研究所推出的研究生培训计划 AMMI 中讲授了一门几何深度学习在线课程——GDL100。目前 2022 年的 GDL100 课程已全部上线，课程视频和讲义等资料均可免费在线查看。课程地址：https://geometricdeeplearning.com/lectures/华为云AI技术领域课程--深度学习https://education.huaweicloud.com/courses/course-v1:HuaweiX+CBUCNXE088+Self-paced/about深度学习是一种以人工神经网络为架构，对数据进行表征学习的算法。目前，在图像、语音识别、自然语言处理、强化学习等许多技术领域中，深度学习获得了广泛的应用，并且在某些问题上已经达到甚至超越了人类的水平。本课程将介绍深度学习算法的知识。

咳咳咳，宝子们！今天我们继续讲解优化算法——指数加权平均数（Exponentially weighted averages）！基本原理小编用脚趾都知道这个优化算法肯定用到了指数加权平均，也可以称之为指数加权移动平均，通过它可以计算局部的平均值，描述数值的变化趋势。所以本篇全文就围绕气温这个案例展开叭~该图表示时间与温度的变化关系，横轴表示一年中的第几天，纵轴表示该天温度，1月份和12月份的温度相对于年中(6月、7月)的温度要低一些。通过温度的局部平均值(移动平均值)来描述温度的变化趋势，平均值计算公式如下：vi表示局部平均值，表示当天的温度，在计算时可把vt看成1/((1-β))的每日温度。这里我们选取三种比较典型的情况来进一步说明：1、假设β等于0.9，计算出10天的温度趋势，如下图的红色曲线。2、假设β接近1，比如0.98，1/(1-0.98)=50，平均了过去50天的温度，如图中的绿线所示。这样的β设置会得到更加平坦一点的曲线，因为我们多平均了几天的温度，所以这个曲线，波动更小，更加平坦，但是会导致曲线进一步右移。换句话说，当β=0.98时，相当于给前一天加了太多的权重，而只有0.02的权重给了当天，所以当β较大时，指数加权平均值适应得更缓慢一些。3、设置β为0.5，这是平均了两天的温度，局部温度平均值如下图黄线部分所示：由于仅仅平均了两天的温度，平均的数据太少，所以得到的曲线有更多的噪声，还有可能出现异常值，不过这个曲线能够更快适应温度的变化。进一步研究其实我们可以不难发现，计算指数加权平均数的关键方程在于：当β=0.9时：以此类推，其实我们完全可以把所有的数值带入并展开：通过上述公式，其实我们可以构建一个指数衰减函数，0.1，0.1×0.9，0.1×(0.9)2，...，这里也可以侧面说明，为什么当β=0.9时只是平均了10天的温度。ε=1-β=1-0.9=0.1，当（1-ε）1/ε=1/e时，即（0.9）10=1/e（e为自然对数），所以当权重下降到峰值权重的1/e时，我们就可以说平均了1/ε=1/1-β天。总体来说，如果想要计算10天局部温度的平均值，我们的常规方法就是需要保存最近10天的温度进行计算；但是使用指数加权平均数优化算法，只需要知道前一个加权平均值是多少就行了（占用极少内存，加快计算速度），当然啦，这样带来的弊端就是精确度可能没有高。偏差修正这个时候，偏差修正就出场了！偏差修正可以提高指数加权平均的精确度，主要针对前期的加权平均值的计算精度。通过计算可以发现，前期的指数加权平均存在较大误差，选用偏差修正可以减少前期指数加权平均的误差。vt/1-βt用来修正指数加权平均的误差，但是随着t的增大，1-βt会趋于1，所以偏差修正对于后期的指数加权平均没有太大影响。总结因此，指数加权平均数这个优化算法经常会被大家拿来使用，通过调整参数（β），可以取得稍微不同的效果，往往中间可能会有某个值效果最好，可以更好地平均数据。那么今天小编的介绍就到此结束啦，欢迎大家多多给小编一点指导意见呀！

接下来就是讲线性模型了。线性模型相对比较简单，但是他是学习比较复杂的深度学习模型的一个基础，而且线性模型本身也具有广泛的用途。 这里讲了线性模型中的线性回归模型和logistic模型。线性回归模型用于处理`回归问题`。logistic模型用于处理`分类问题`。 线性回归模型可以写作如下的形式：  其中那`一系列的x`都是已知，而且比较容易测量到的向量。`一系列的w`是权重或者叫做系数。`b`是一个常数，叫做截距或偏差。$\boldsymbol\epsilon$ 是误差，代表了没有在x里体现但对y有影响的信息。 这其中一系列的w和b都是未知数，就是`模型参数`。

然后就是Python的介绍。包括常见的数据类型，基本算术运算，比较和布尔运算，如何载入额外的模块和包。 基本数据结构有列表、元组、字典和集合。控制结构，内建函数和自定义函数。 然后介绍numpy库，他可以实现快速的算数运算，特别是矩阵运算，运算内部是通过C语言实现的，所以比较快。他包含两种基本数据类型：`数组（array）`和`矩阵（matrix）`。 然后介绍基于numpy库的pandas库，可以用于数据分析，数据清理和数据准备。他的数据结构主要有两种：`序列（series）`和`数据表（dataframe）`。 画图工具mathplotlib是在Python中最流行的，可以很方便的实现数据的图形化展示。使用前要载入mathplotlib的`pyplot`。 其实这些知识在华为云的AI gallery里面都有相应的入门教程。

接下来是概率论的一些基本的概念。 `随机变量`就是一个取值不确定的变量。 这个在工作生活中应用的实在是太广泛了。比如老板问你这件事情明天能不能搞完？一般情况下，你的回答可能就是一个随机变量。 随机变量可以分为两种类型：连续型和离散型。 `随机变量的分布`用来描述随机变量出现某种结果的可能性。可以用一些分布函数来表示。 常见的概率分布有几种。这里只看最常见的一种概率分布，就是`正态分布`也叫高斯分布。 很多情况下，还有一种叫做`条件概率`。就是我们会关心当A事件发生时，B事件发生的概率。在生活中也是经常有场景的，比如当小孩长时间的磨磨唧唧的做事的时候，你发火的概率。 `Anaconda`，用于管理和隔离环境`env`。因为在实际中我们经常会需要用到不同的版本的python，甚至于特定版本的python模块包。这种情况下就非常好用，可以让这些环境共存。Anaconda帮你管理了。命令是`conda`，具体使用和功能参数就不说了。 `Jupyter Notebook`是WEB应用，可方便的创建、运行和分享python代码。conda install jupyter notebook就可以安装。安装好启动后就自动打开网页，就可以使用了。ctl-c按2次可以退出。有命令模式和编辑模式。有代码框和标记框（`markdown cell`）。

最常用的矩阵运算是矩阵的转置。转置就像是翻转。就像是一个扑克牌，原来是竖着拿的，把它变成翻面横着拿了。  矩阵的基本运算就是加减乘除。加减法如果这两个矩阵的维度是一样的，就非常好理解。矩阵也可以和行向量进行加减，要求行向量的列数和矩阵的列数是一样的。 矩阵的乘法，如果两个矩阵的维度一样，也非常好理解，这种叫做`逐点相乘`（element-wise product）。 还有一种惩罚就是我们在线性代数中的乘法。叫做`点乘`。点乘是这样的：  然后是向量和矩阵的范数，不好理解。 还有微积分的导数和求导法则，也不好看。

嗨咯，宝子们，每周一见！今天给大家带来一些优化算法。优化算法，顾名思义，小编猜应该是帮忙我们训练模型优化，提高训练速度的方法。废话不多说，今天就给大家科普一下Mini-batch梯度下降法~如何使用在我们之前的介绍中，m个样本其实是看作向量方便大家较快处理计算的，因此，我们把训练样本放到矩阵X中进行处理：X=[x(1) x(2) x(3) ……x(m) ]，同理，Y也是如此，Y=[y(1) y(2) y(3)……y(m) ]，X的维数是(nx,m)，Y的维数是(1,m)。当然，这里有个前提，就是m的数值不会很大，否则依然处理速度缓慢。那么这个时候，我们就可以借助梯度下降法提前处理一部分数据。可以把训练集分割为小一点的子集训练，这些子集我们可以称之为mini-batch。假设每一个子集中只有1000个样本，那么把其中的x(1)——x(1000))提取出来，将其称为第一个子训练集，也叫做mini-batch，然后再取出x(1000)——x(2000)，以此类推。这里为了方便更好地统计，X{1}=x(1)——x(1000))，X{2}=x(1000)——x(2000)X^({2})，假设训练样本m=500w，每个mini-batch都有1000个样本，也就是说，这个训练集一共有5000个mini-batch。对于Y的处理也是同样的，拆分Y的训练集，对应地，Y{1}=y(1001)——y(2000)，Y{2}，...，Y{5000}。mini-batch的数量t组成了X{t}和Y{t}，包含相应的输入和输出，这里的t就表示不同的mini-batch。X{t}和Y{t}的维数：X{t}所有维数都是(nx,1000)，而Y{t}的维数都是(1,1000)。那么mini-batch梯度下降法的原理是什么样的呢？在训练集上运行mini-batch梯度下降法，运行：for t=1……5000，在for循环里对X{t}和Y{t}执行一步梯度下降法。假设有一个拥有1000个样本的训练集，要用向量化去几乎同时处理1000个样本。首先对输入X{t}，执行前向传播，然后执行z[1]=W[1]X+b[1]，而处理第一个mini-batch时就全部转成X{t}，即z[1]=W[1] X{t}+b[1]，然后执行A[1]k=g[1](Z[1])，以此类推，直到A[L]k=g[L](ZL])，也就是我们的预测值。这样一个向量化的执行命令一次性处理1000个而不是500万个样本。接下来就是执行反向传播来计算J{t}的梯度，更新加权值，W[l]:=W[l]-adW[l]，b[l]:=b[l]-adb[l]，这是使用mini-batch梯度下降法训练样本的一步，也可被称为进行“一代”（1 epoch）的训练。一代表示一次遍历了训练集。使用batch梯度下降法，一次遍历训练集只能做一个梯度下降，而使用mini-batch梯度下降法，一次遍历训练集，能做5000个梯度下降，因此，mini-batch梯度下降法比batch梯度下降法运行地更快。当然也可以一直处理遍历训练集，直到最后能收敛到一个合适的精度。进一步理解使用batch梯度下降法时，每次迭代都需要历遍整个训练集，可以预期每次迭代成本都会下降，所以如果成本函数J是迭代次数的一个函数，它应该会随着每次迭代而减少，如果J在某次迭代中增加了，那肯定出了问题，也许学习率太大。使用mini-batch梯度下降法，我们会发现成本函数并不是每次迭代都是下降的，特别是在每次迭代中，我们要处理X{t}和Y{t}，成本函数J{t}的只和X{t}、Y{t}有关，最终我们会发现，图像整体走向朝下，但是有更多的噪声，我们需要决定的变量之一是mini-batch的大小，m指训练集的大小，其实如果mini-batch的大小等于m，就是batch梯度下降法，这样的话我们就有了mini-batchX{1}和Y{1}，并且该mini-batch等于整个训练集。当然还可以假设mini-batch大小为1，这样就变成了随机梯度下降法，每个样本都是独立的mini-batch，第一个mini-batch就是第一个训练样本，接着是第二个mini-batch，也就是第二个训练样本，以此类推，一次只处理一个。从上图中我们可以发现，在两种极端下成本函数的优化情况：1、batch梯度下降法从某处开始，相对噪声低些，幅度也大一些，但可以继续找最小值；2、而在随机梯度下降法中，从某一点开始，每次迭代只对一个样本进行梯度下降，大部分时候会向着全局最小值靠近，因此随机梯度下降法是有很多噪声的，它最终会靠近最小值，不过有时候也会方向错误，因为随机梯度下降法永远不会收敛，而是会一直在最小值附近波动。实际上我们选择的mini-batch大小应该在在1和m之间，如果使用batch梯度下降法，mini-batch的大小为m，每个迭代需要处理大量训练样本，该算法的主要弊端在于训练样本数量巨大的时候，单次迭代耗时太长；相反，如果使用随机梯度下降法，通过减小学习率，噪声会被改善或有所减小，但随机梯度下降法的一大缺点是，会失去所有向量化带来的加速，因为一次性只处理了一个训练样本。所以实际上一些位于中间的mini-batch大小效果最好，这里有个小技巧可以无偿赠送给大家！1、如果训练集较小，直接使用batch梯度下降法（小于2000个样本）2、样本数目较大的话，一般的mini-batch大小为64到512（设成2的次方）3、需要确保X{t}和Y{t}和CPU/GPU内存相匹配当然啦，优化算法肯定不止这一个，我们后续会给大家继续带来讲解！再见不送~

深度学习(DL, Deep Learning)是机器学习(ML, Machine Learning)领域中一个新的研究方向，它被引入机器学习使其更接近于最初的目标——人工智能(AI, Artificial Intelligence)。深度学习是学习样本数据的内在规律和表示层次，这些学习过程中获得的信息对诸如文字，图像和声音等数据的解释有很大的帮助。它的最终目标是让机器能够像人一样具有分析学习能力，能够识别文字、图像和声音等数据。 深度学习是一个复杂的机器学习算法，在语音和图像识别方面取得的效果，远远超过先前相关技术。深度学习在搜索技术，数据挖掘，机器学习，机器翻译，自然语言处理，多媒体学习，语音，推荐和个性化技术，以及其他相关领域都取得了很多成果。深度学习使机器模仿视听和思考等人类的活动，解决了很多复杂的模式识别难题，使得人工智能相关技术取得了很大进步。自下上升的非监督学习就是从底层开始，一层一层地往顶层训练。采用无标定数据（有标定数据也可）分层训练各层参数，这一步可以看作是一个无监督训练过程，这也是和传统神经网络区别最大的部分，可以看作是特征学习过程。具体的，先用无标定数据训练第一层，训练时先学习第一层的参数，这层可以看作是得到一个使得输出和输入差别最小的三层神经网络的隐层，由于模型容量的限制以及稀疏性约束，使得得到的模型能够学习到数据本身的结构，从而得到比输入更具有表示能力的特征；在学习得到n-l层后，将n-l层的输出作为第n层的输入，训练第n层，由此分别得到各层的参数。自顶向下的监督学习就是通过带标签的数据去训练，误差自顶向下传输，对网络进行微调。基于第一步得到的各层参数进一步优调整个多层模型的参数，这一步是一个有监督训练过程。第一步类似神经网络的随机初始化初值过程，由于第一步不是随机初始化，而是通过学习输入数据的结构得到的，因而这个初值更接近全局最优，从而能够取得更好的效果。所以深度学习的良好效果在很大程度上归功于第一步的特征学习的过程。